probleme maths exercice fonction terminale

Lors d'une expérience en laboratoire, on lance un projectile dans un milieu fluide. L'objectif est de déterminer pour quel angle de tir θ par rapport à l'horizontale la hauteur du projectile ne dépasse pas 1,10 mètre.
Comme le projectile ne se déplace pas dans l'air mais dans un fluide, le modèle parabolique usuel n'est pas adopté.
On modélise ici le projectile par un point qui se déplace, dans un plan vertical, sur la courbe représentative de la fonction f définir sur l'intervalle [0;1[ par :f(x)=2ln(1−x)+bx où b est un paramètre réel supérieur ou égal à 2, x est l'abscisse du projectile, f(x) son ordonnée, toutes les deux exprimées en mètres.

La fonction f est dérivable sur l'intervalle [0;1[. On note f′ sa fonction dérivée.
On admet que la fonction f possède un maximum sur l'intervalle [0; 1[ et que, pour tout réel x de [0;1[ :
f′(x)=-2/(1-x)+b
Exprimer le maximum de la fonction f en fonction de b.
Déterminer pour quelles valeurs du paramètre b la hauteur maximale du projectile ne dépasse pas 1,10 mètre.
On donnera la réponse sous la forme d'un ensemble, par exemple {1;3} ou[2;4[, avec une précision au dixième.
Dans cette question, on choisit b = 3,58.
L'angle de tir θ correspond à l'angle entre l'axe des abscisses et la tangente à la courbe de la fonction f au point d'abscisse 0 comme indiqué dans le schéma donné ci-dessus.
Déterminer une valeur arrondie au dixième de degré près de l'angle θ.

Bonjour mimims, (Marque de politesse à ne pas oublier !!)

Réduis l'expression de $f^{'} (x)$ au même dénominateur et résous $f^{'} (x) = 0$ .
Des variations de la fonction, tu déduis le maximum.

@Noemi Bonsoir,

ce n'était pas cette question que je n'arrivais pas mais la 2 et 3. Sinon pour la 1 j'avais trouvé x=-2/b+1

@mimims et aprés il suffisait de faire f(x) que j'ai trouvé

Si tu as terminé l'exercice, c'est bien.
N'oublie pas la prochaine fois de préciser la question qui te pose problème.

Bonjour,

@mimims , comme te l'a indiqué @Noemi , si tu ne dis pas ce qui te pose problème, on peut pas te répondre utilement.

Pour que tu puisses vérifier la 2) et la 3), je t'indique des résultats :

Sauf erreur,

Pour la 2) : $4.8]b\in[ 2, \ 4.8]$

Pour la 3) : $f′(0)=tan(θ)=1.58f'(0)=tan(\theta)=1.58$

à 0.1 près par défaut, $θ≈57.6\theta \approx 57.6$ °

@mtschoon, Bonjour en effet je pensais l'avoir écris. Mais sinon je n'ai pas compris comment trouvé les réponses 2 et 3

Pour la question 2), utilise le résultat de la question 1) sachant que le maximum ne dépasse pas 1,10 m.
Tu résous l'inéquation ou tu cherches la solution à l'aide de la calculatrice.

Pour la question 3) mtschoon a indiqué le calcul.

@mimims ,

Quelques détails pour la 2),

Tu sais que d'après 1) le maximum de f est
$f(−2b+1)=b−2+2ln(2b)f(-\dfrac{2}{b}+1)=b-2+2ln(\dfrac{2}{b})$ pour $b≥2b\ge 2$

A la 2) tu dois donc chercher b tel que :
$b−2+2ln(2b)≤1.10\boxed{b-2+2ln(\dfrac{2}{b})\le 1.10}$

Je te conseille de poser $g(b)=b−2+2ln(2b)g(b)=b-2+2ln(\dfrac{2}{b})$ , b étant la variable appartenant à $[2,+∞[[2,+\infty[$

Tu étudies les variations de g

Après calcul :
$g′(b)=b−2bg'(b)=\dfrac{b-2}{b}$

d'où

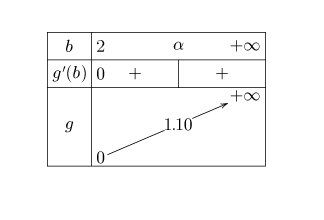
En utilisant le TVI, tu prouves qu'il existe une valeur unique $α\alpha$ de $[2,+∞[[2,+\infty[$ telle $g(α)=1.10g(\alpha)=1.10$

Tu cherches des valeurs approchées de $α\alpha$ à la calculette.
g(4.8)=............
g(4.9)=............

Tu tires la conclusion (indiquée dans ma réponse précédente)

Pour la question 3), demande si ma réponse précédente n'est pas suffisante.

Bon travail.

Ce message a été supprimé !

j'ai une question pour la 3) pourquoi f'(0)=tan(teta)

Pour la question 3,
Le nombre dérivée en 0, correspond au coefficient directeur de la tangente. C'est aussi la tangente de l'angle.

@Noemi merci bien !