Fonction strictement croissante ou non sur R

Bonsoir tout le monde, je bloque vraiment sur un exercice. Est-ce vous pouvez m’aider svp ?

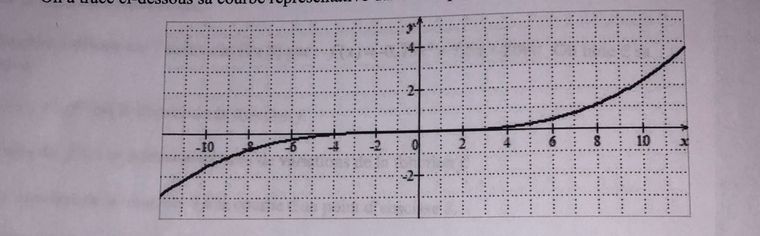
Énoncer : On considère une f définie sur R par f(x) = 0,002x^3 + 0,003x^2 - 0,012x + 0,0015.

On a tracé ci-dessus sa courbe représentative dans un repère.

Cette fonction est-elle strictement croissante sur R ? Justifier.

Bonsoir Kenza-Mansouri ,

Calcule la dérivée de la fonction est vérifie si $f (x) = 0$ a une solution.

Ce message a été supprimé !

@Noemi Bonsoir, merci.

Je l’ai dérivée et j’ai trouvé ça :
F(x) = 0,002x³ + 0,003x²- 0,012x + 0,0015.

F’(x)= 0,002 x 3x² + 0,003 x 2x - 0,012 + 0

F’(x)= 0,006x² + 0,006x - 0,012
La dérivée est-elle correcte ?

Maintenant je dois résoudre ?

La dérivée est correcte. Résous $f^{'} (x) = 0$ .

Bonjour,

@Kenza-Mansouri ,

Lorsque tu auras résolu $f^{'} (x) = 0$ , il te faudra chercher le signe de $f^{'} (x)$ pour $\in R$ pour pouvoir tirer la conclusion.

Propriété que je te rappelle :
Soit f une fonction dérivable sur un intervalle I.
Si f ’ est strictement positive sur I, sauf éventuellement en un nombre fini de réels x de I pour lesquels f ’ (x) = 0, alors f est strictement croissante sur I.
Si f ’ est strictement négative sur I, sauf éventuellement en un nombre fini de réels x de I pour lesquels f ’ (x) = 0, alors f est strictement décroissante sur I.

Remarque : le graphique est volontairement trompeur, car on ne peut pas vraiment voir ce qui se passe exactement pour les valeurs de x voisines de 0 (on pourrait même penser que la fonction est peut-être constante dans un intervalle entourant 0...)

F' (x) = 0,006x² + 0,006x - 0,012 = 0
Discriminant= b² - 4ac
Discriminant= 0,006² - 4x 0,006 x (-0,012)= 3,24 x 10^-4
Donc, l'équation f'(x) = 0 admet aucune solution.

Le coefficient de x² égal à 0,006, est positif.

                x                                               - infini                                           + infini      
                                                                                                +

f'(x) = 0,006x² + 0,006x - 0,012

La fonction est donc strictement croissante sur R ?

Désolée pour ce tableau très mal fait

Le discriminant est positif, donc l'équation admet deux solutions.

Mince c’est vrai !
Du coup :
X1= -b + √ Δ / 2a
X1= -0,006+ √3,24x 10^-4 / 2x0,006
X1= -0,005946

X2= -b - √ Δ / 2a
X2= -0,006 - √3,24x 10^-4 / 2x0,006
X2= -0,006054

   X	      - ♾                 +♾
 F’(x)	                +

@Kenza-Mansouri , les solutions de f'(x)=0 sont fausses.
Recompte.

Remarque : en prenant des expressions fractionnaires, c'est plus simple :

$f′(x)=61000x2+61000x−121000f'(x)=\dfrac{6}{1000}x^2+\dfrac{6}{1000}x-\dfrac{12}{1000}$

$f′(x)=61000(x2+x−2)=3500(x2+x−2)f'(x)=\dfrac{6}{1000}(x^2+x-2)=\dfrac{3}{500}(x^2+x-2)$

$f^{'} (x) = 0$ <=> $x^2+x-2=0$

Les calculs seront plus faciles

Est-ce que les solutions sont 1 et -2 ?

Oui, ce sont les solutions.

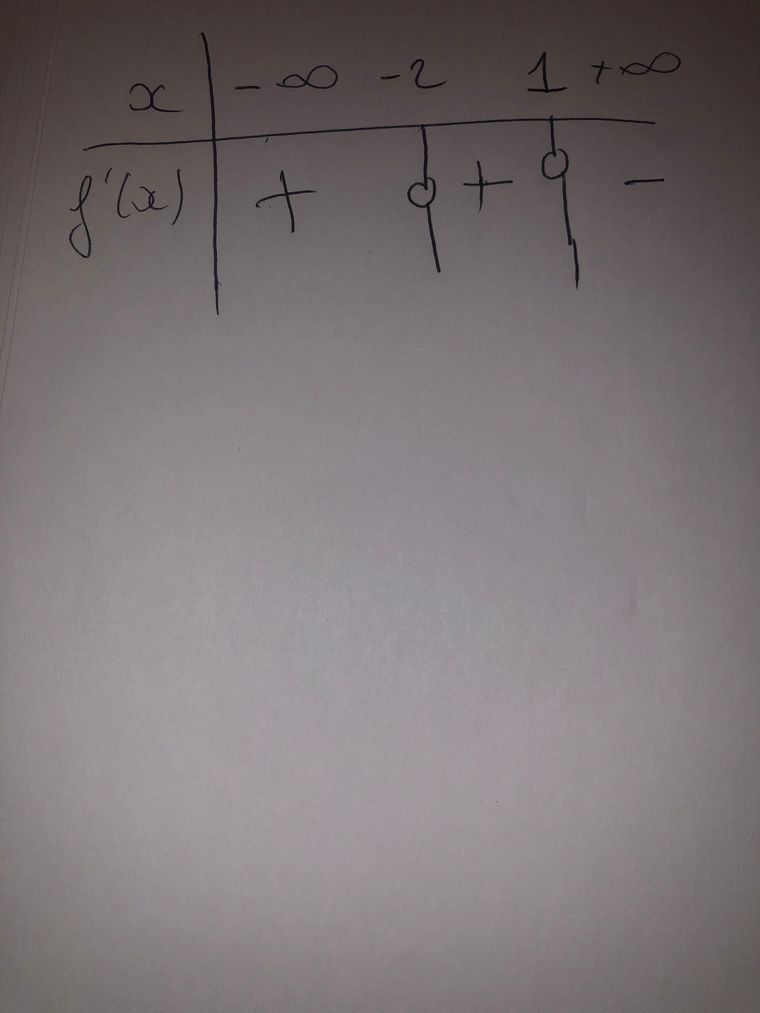Est-ce que c’est correct ?

C'est faux, indique tes calculs.

@Kenza-Mansouri ,

1 et -2 sont bien les solutions de f'(x)=0

Je te conseille de revoir ton cour sur le signe d'un polynôme du second degré.

Rappel :
soit $g(x)=ax^2+bx+c$ avec $a≠0a\ne 0$

soit $x_1$ et $x_2$ les solutions de $g (x) = 0$ avec $x1<x2x_1\lt x_2$

Pour x à "l'extérieur" des racines, c'est à dire pour $x<x1x\lt x_1$ et pour $x>x2x\gt x_2$ , g(x) est du signe de a

Pour x "entre les racines ", c'est à dire $x1<x<x2x_1\lt x\lt x_2$ , g(x) est du signe de -a.

Donc ..........................(tu revois ta réponse)

Une remarque : lorsque tu auras terminé correctement de traiter ton exercice par l'étude générale de la fonction f, je t'indiquerais une méthode rapide qui t'aurais permis de répondre à la question posée sans faire l'étude générale de la fonction.

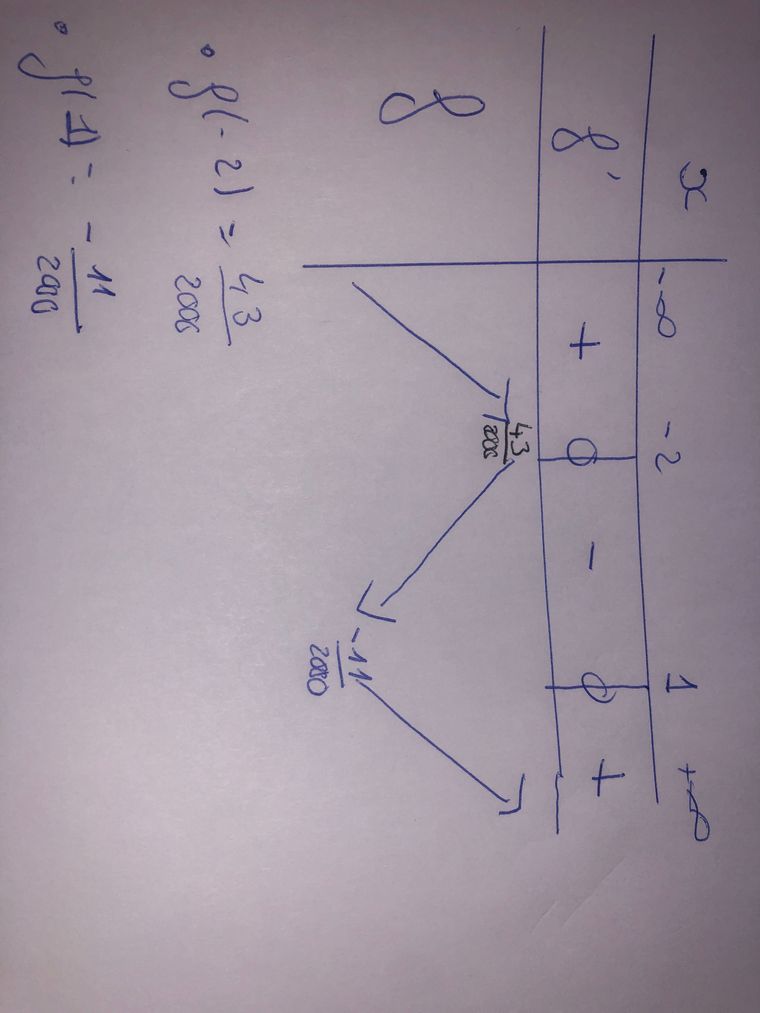Merci beaucoup, j’ai rectifié. Est-ce que c’est juste ?

@Kenza-Mansouri ,

Les signes sont bons et le sens de variation aussi.

Les valeurs de f(-2) et de f(1) sont peut-être à revoir...vérifie.

ma calculette me donne f(-2)=0.0215 et f(1)=-0.0055

Oui, elle me donne pareil, mais c’est parce que j’ai mis en fraction. Du coup je conclus en disant que la fonction n’est pas strictement croissante sur R: elle est croissante entre -♾ et -2, puis devient décroissante entre -2 et 1, pour être à nouveau croissante a partir de 1 ?

@Kenza-Mansouri ,

Oui, mais tu peux préciser "strictement croissante" ou "strictement décroissante" au lieu de "croissante" ou "décroissante", vu que sur les intervalles considérés, la dérivée est strictement positive ou strictement négative.

Merciii vous m’avez été d’une grande aide !!

@Kenza-Mansouri , de rien !
C'est très bien si tu maîtres bien l'étude de la fonction. C'est indispensable de savoir le faire.

Comme je te l'ai indiqué en remarque dans une réponse précédente, tu aurais pu répondre à la question sans faire l'étude générale, en trouvant seulement un contre-exemple.
Je t'indique cette seconde méthode (très rapide)

En regardant le schéma donné dans ton énoncé, c'est pour x compris entre -2 et 2 que l'on ne voit rien de précis et qu'on se demande même si entre ces 2 valeurs la fonction ne serait pas constante.
On peut donner à x quelques valeurs simples, par exemple -2,-1,0,1,2 et ,à la calculette, calculer f(-2),f(-1),f(0), f(1), f(2), pour voir ce qui se passe.

Par exemple:
$−2<0\boxed{-2 \lt 0}$
$f (- 2) = 0.0215$ et $f (0) = 0.0015$ donc $f(−2)>f(0)\boxed{f(-2) \gt f(0)}$
Donc f ne peut pas être strictement croissante sur R grâce à cet exemple (appelé contre-exemple)

Voilà une méthode rapide...

Bonne réflexion.