Taux d’alcoolémie, calcul dérivée

Bonjour à tous, je bloque énormément sur cet exercice, je n’ai rien commencé car je n’y arrive pas. Pourrais-je avoir votre aide s’il vous plaît ?

Énoncer:

Une étude sur un jeune homme de 64kg ayant ingéré une dose de 33g d’alcool a permis d’établir que le taux d’alcool dans le sang, en fonction du temps t en heure, est donné par la fonction f définie sur l’intervalle
[0;+∞[ par:

f(t)= (2t−0,05)e^-t

La représentation graphique de cette fonction dans un repère orthonormé est donnée ci-dessous:

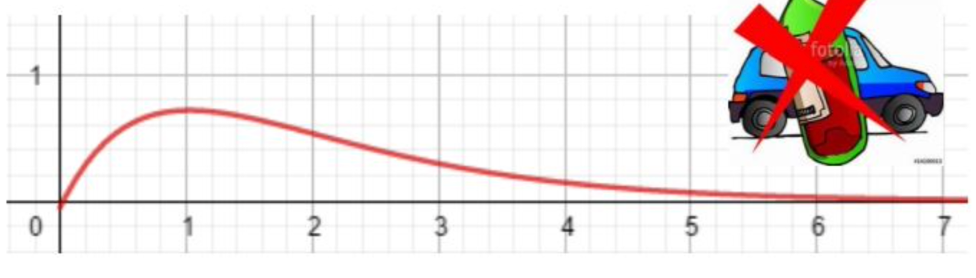
Questions:
1 ) Avec la précision permise par le graphique, déterminer combien de temps après l’ingestion le taux d’alcool passe au-dessous du seuil de 0,25 g.L−1

2)Un taux d’alcool dans le sang inférieurà0,001 g.L−1 estconsidéré comme négligeable.
En complétant, puis en utilisant le programme écrit en python ci-dessous, déterminer à partir de combien de temps ( à 10−2 près) le taux d’alcool dans le sang du jeune homme est négligeable ?

Déterminer le tableau de variation de f .
En déduire une valeur approchée au centième du taux maximum d’alcool dans le sang du jeune homme.

Je vous mets le lien de l’exercice, juste pour que vous puissiez voir le graphique et le tableau.

http://pierrelux.net/documents/corrections/500000/500320.JPG

Bonjour Theo-Dutoo,

Question 1) Place sur l'axe des ordonnées 0,25, puis tu traces la droite $y = 0, 25$ . détermine l'abscisse du deuxième point d'intersection de la droite et de la courbe.

Question 2) Utilise le programme Python.

Question 3) Calcule la dérivée de la fonction.

Indique ta réponse si tu souhaites une vérification.

Pour la question 1) j’ai trouvé environ 3H

Pour la question 2) Je n’y arrive pas

Pour la question 3)

F(t)= (2t-0,05) e^ -t
F’(t)= (2-0) 3^ -t ?

@Theo-Dutoo

c'est 3h ou 3h12min.
il manque le programme Python dans l'énoncé.
La dérivée est $f'(t) = 2e^{-t}-(2t-0,05)e^{-t} = .....$
Simplifie l'écriture de la dérivée puis tu étudies le sens de variation.

@Noemi a dit dans Taux d’alcoolémie, calcul dérivée :

2e−t−(2t−0,05)e−t

Pourquoi ce n’est pas 2e^ -t + (2t - 0,05) e^ -t ?

@Theo-Dutoo

Tu appliques la dérivée de $U×VU\times V$
Soit $U′×V+U×V′U'\times V + U\times V'$
$V = e^{-t}$ et $V'=-e^{-t}$ d'ou le signe moins .

@Theo-Dutoo

U’ = 2 ?

@Theo-Dutoo
Oui
$U = 2 t - 0, 05$ et $U^{'} = 2$ .

D’accord merci.

Alors e^-t ( - 2t + 0,05) ?

@Theo-Dutoo

Oui si cela correspond à $U×V′U\times V'$

Je n’ai pas bien compris, vous m’avez dit de simpifier :

F’(t) = 2e^-t - (2t - 0,05) e ^ -t

Ainsi F’(t) = e^-t ( -2t + 0,05) est-ce bien cela ?

Car on m’a aussi dit que ; F’(t)= e^-t (2,05 - 2t) du coup je suis un peu embrouillé.

@Theo-Dutoo

$f'(t) = 2e^{-t}-(2t-0,05)e^{-t} =(2-2t+0,05)e^{-t}= (2,05-2t)e^{-t}$

Ok merci. Ensuite je résous 2,05 - 2t= 0
2,05= 2t
t= 2,05 / 2
t= 1,025

Js fais un tableau allant de 0 à + infini

Mais ensuite je n’y arrive pas.

@Theo-Dutoo

Pour le tableau de variation
$x$ 0 puis 1,025 puis $+∞+\infty$
Signe de $f^{'} (t)$ + 0 -
variation de $f$ flèche vers le haut (croissante) puis flèche vers le bas (décroissante)

Pour la question 4, calcule $f (1, 025)$ .

Dans le tableau f, je met un chiffre entre les 2 flèches ? Et f’1,025 = 0

Ensuite pour la 2, j’ai rempli le tableau :

1 from math import exp
2 x=1
3 while (2*x-0.05)*exp(-x) > 0,001
4 x= x+0,01
5 print(x)

Est-ce juste ?

@Theo-Dutoo

Pour le tableau de variation la valeur entre les deux flèches est $f (1, 025) = . . . . .$

Pour le programme Python qui est juste, tu peux commencer à $x = 3$ , vu que tu as trouvé 3 h à la première question.