Tableau de variation d'une fonction carrée pour Seconde

Bonjour ,

Est-ce que quelqu'un pourrait m'expliquer le tableau de variation d'une fonction carrée suivant svp ?

X/-oo 0 +oo
f/+oo 0 +oo

Bonjour Sakura-kikuchi,

Comment étudies tu les variations d'une fonction ?

Si $f(x) = x^2$
Calcul du rapport : $f(x2)−f(x1)x2−x1=...\dfrac{f(x_2)-f(x_1)}{x_2-x_1}= ...$

Bonjour,

@Sakura-kikuchi , ta question n'est pas claire.

S'il s'agit de faire les calculs pour démontrer le sens de variation de la fonction, suit la piste de @Noemi
Tu trouveras :
que pour x négatif, la fonction est décroissante
que pour x positif, la fonction est croissante
que le minimum est pour x=0 et vaut 0

S'il s'agit de comprendre comment est fait le tableau de variation , je tente une explication :

a) x prend des valeurs réelles : $x∈]−∞,+∞[x\in ]-\infty,+\infty[$
C'est la ligne indiquée pour x.
On met 0 sur cette ligne vu que le minimum est pour x=0

Lorsque x prend des valeurs négatives très grandes en valeurs absolues, f(x) prend des valeurs positives très grandes en valeurs absolues,
exemple : pour $x = - 100$ , $f (x) = + 10000$

Ainsi, sur la ligne de f, on met $+∞+\infty$ juste au dessous de $−∞-\infty$ (pour x)
On dit que lorsque x tend vers $−∞-\infty$ , f(x) tend vers $+∞+\infty$

b) De même, tu peux faire le même raisonnement lorsque x prend des valeurs positives très grandes en valeur absolue.
Pour x=+100, f(x)=+10000
Lorsque x tend vers $+∞+\infty$ , f(x) tend vers $+∞+\infty$

c) Lorsque $x = 0$ , $f(x)=0^2=0$
On met donc un $0$ sur la ligne de $f$ juste au dessous du $0$ (pour x)

d) Lorsque x varie de $−∞-\infty$ à $0$ , f est décroissante et varie de $+∞+\infty$ à 0 : on met une flèche qui descend

e) Lorsque x varie de $0$ à $+∞+\infty$ à $0$ , f est croissante et varie de $0$ à + $∞\infty$ : on met une flèche qui monte.

La représentation graphique de la fonction carrée (parabole) , illustre tout cela :

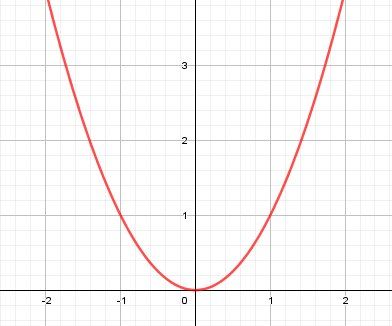
Reposte si l'on a pas répondu précisémment à la question que tu poses.

@mtschoon mercii c'était exactement ça ma question

@Sakura-kikuchi , c'est parfait si tu as bien compris ; demande si tu as un doute .

@mtschoon okiii merciiii

@Sakura-kikuchi , de rien !
Bon travail.