Equation avec des valeurs absolues

Bonsoir tout le monde
|1-5x|=|x-1|
x=1/5 x=1
]-oo,1/5[
-1+5x=-x+1
x=1/3 N'APPARTIENT pas à l'intervalle
]1/5,1[
1-5x=-x+1
x=0 N'APPARTIENT pas à l'intervalle
]1 +oo[
1-5x=x-1
x=1/3 N'APPARTIENT pas à l'intervalle
Si x= 1/5
|1-5x|=|x-1|
|1-5(1/5)|=|1/5-5/5
|0|=|-4/5| faux
Si x=1
|1-5x|=|x-1|
|1-5|=|1-1|
|-4|=|0| faux
S=l'ensemble vide

Bonjour Sakura-kikuchi ,

Revoir la résolution de l'inéquation $\gt0$
Un lien vers un site : https://www.youtube.com/watch?v=jBXUaLFb2nY
ou : https://www.youtube.com/watch?v=KwNENJ_NcVI

Exact mtschoon, Lecture réponse trop rapide.

Bonjour,

Noemi a écrit :
"Noemi MODÉRATEURS il y a environ 37 minutes
Bonsoir Sakura-kikuchi ,
C'est correct."

Non, ce n'est pas correct.
Visiblement, l 'erreur de @Sakura-kikuchi n'a pas été vue par @Noemi .

@Sakura-kikuchi , tu dois revoir le signe de (1-5x) suivant x, pour donner correctement les expressions de |1-5x| qui sont inexactes.

Lorsque tu auras refait le travail , tu dois trouver que les solutions de l'équation proposée sont $0$ et $13\dfrac{1}{3}$

Remarque : Lorsque tu auras refait ton exercice, je te proposerai une autre méthode plus rapide, si tu le souhaites.

@Noemi , bonjour,

Effectivement, tu as eu une "lecture trop rapide" hier soir, mais ça arrive de ne pas tout voir ...

Tu as bien fait de modifier ta réponse ce matin , après mon intervention !

@Sakura-kikuchi , je te détaille ton erreur sur le signe de $1 - 5 x$ qui fausse tout ton exercice.

$1−5x<0\boxed{1-5x \lt 0}$ <=> $\lt -1$
Lorqu'on divise par un nombre négatif, on change le sens de l'inégalité

donc : $\lt -1$ <=> $x>−1−5x\gt \dfrac{-1}{-5}$ <=> $x>15\boxed{x\gt \dfrac{1}{5}}$

Remarque :
Tu peut aussi décomposer le calcul en deux temps, si ça te parait plus clair à comprendre :
$1−5x<0\boxed{1-5x \lt 0}$ <=> $\lt -1$

Lorsqu'on change les signes (en multipliant par (-1)) , on change sens de l'inégalité :
$\lt -1$ <=> $5x>15x\gt 1$

on divise ensuite par 5 (qui est positif) :
$x>15\boxed{x\gt \dfrac{1}{5}}$

Evidemment, de la même façon :
$1−5x>0\boxed{1-5x\gt 0}$ <=> .....<=> $x<15\boxed{x\lt \dfrac{1}{5}}$

@Noemi merci beaucoup je vais de ce pas regarder la vidéo et rectifier mon erreur

@mtschoon d'accord merciii je vais regarder la video de @Noemi après je reporterai l'équation pour une correction ensuite vous pourriez m'indiquer la méthode plus rapide si ça vous dérange pas

@mtschoon d'accord je vais rectifier ça mercii bcp

@Sakura-kikuchi

J'ai indiqué deux sites possibles pour voir des exemples de résolution.

@Sakura-kikuchi , je t'indique la méthode rapide , vu que tu la souhaites.

Deux expressions ayant la même valeur absolue sont ou bien égales ou bien opposées, c'est à dire
|A|=|B| <=> A=B ou A=-B

Ici,
Premier cas
$1 - 5 x = x - 1$ <=> $- 6 x = - 2$ <=> $x=−2−6x=\dfrac{-2}{-6}$ <=> $x=13\boxed{x=\dfrac{1}{3}}$

Second cas
$1 - 5 x = - (x - 1)$ <=> $1 - 5 x = - x + 1$ <=> $- 4 x = 1 - 1$ <=> $- 4 x = 0$ <=> $x=0\boxed{x=0}$

@Sakura-kikuchi ,

Tu peux faire une vérification graphique des réponses avec ta calculette graphique.
$f (x) = ∣ 1 - 5 x ∣$ (représentation en vert)
$g (x) = ∣ x - 1 ∣$ (représentation en rouge)

Les solutions de f(x)=g(x) sont les abscisses des points d'intersection de deux représentations graphiques :
A a pour abscisse 0
B a pour abscisse $13\frac{1}{3}$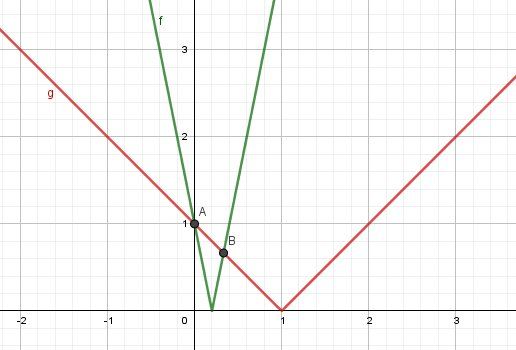

Bonne réflexion.

@mtschoon cette méthode est plus et plus rapide mercii bcp

@Noemi oui je veux bien

@Sakura-kikuchi ,

Oui , la méthode "rapide" est bien plus simple, c'est sûr.

Je te conseille, pour bien apprendre, de faire les deux méthodes et de vérifier que tu trouves le même ensemble de solutions.

Cela te permettra de bien maîtriser les valeurs absolues.

@mtschoon est ce que cette méthode est aussi valable quant on a une équation du type
|a|+|b|=c
Genre je peux résoudre en disant
a+b=c ou a+b=-c

@mtschoon d'accord je vais faire ça merci encore pour vos aides

@Sakura-kikuchi , non à ta proposition sur |a|+|b|=c

C'est pour cela que je te conseille d'approfondir en réfléchissant.

Lorsque tu écris |a|+|b|=c, ce n'est pas de la forme |A|=|B|

|a|+|b| n'est pas une valeur absolue mais la somme de deux valeurs absolues ( et la valeur absolue d'une somme n'est pas égale à la somme des valeurs absolues).
De plus, tu ne dis rien sur c. On ne sait pas s'il est positif ou négatif, et il n'y a pas la valeur absolue.

Contente toi d'utiliser la méthode courte, si tu le souhaites, seulement lorsque tu as l'égalité de deux valeurs absolues.

@mtschoon d'accord

@Sakura-kikuchi , bon travail !

@mtschoon