Résolution dans R d'une équation avec des valeurs absolues
-
Sakura kikuchi dernière édition par Noemi

Coucou ,j'espère que vous allez bien j'ai besoin d'une correction ...il s'agit de la résolution dans R j'ai aussi une question à ce sujet
|x+7|-|4x-1|=3|×+7|= ×+7 > 0 , × > -7
|×+7|= -×-7 < 0 ,-× < 7, × > 7|4×-1| = 4×-1 >0 , × > 1/4
|4×-1|= -4×+1<0 , × > 1/4]-oo -7[
-×-7-(-4×+1)=3
×=11/3 N'APPARTIENT pas]-7,1/4[
×+7-(-4×+1)=3
×=-3/5 appartient à l'intervalle
]1/4 +oo[
×+7-(4×-1)=3
×=5/3 appartient à l'intervalle
Voila arriver à ce niveau là est ce que j'ai besoin de vérifier si x=-7 et si ×=1/4 font parti des solutions de l'équation?
-
Bonsoir Sakura-kikuchi,
Des erreurs au début :
∣x+7∣=x+7\vert x+7\vert=x+7∣x+7∣=x+7 si x+7≥0x+7\geq0x+7≥0 soit x≥−7x\geq-7x≥−7
∣x+7∣=−x−7\vert x+7\vert=-x-7∣x+7∣=−x−7 si x+7≤0x+7\leq0x+7≤0 soit x≤−7x\leq-7x≤−7Idem pour l'autre valeur absolue.
Le reste est juste.
Ecris l'ensemble solution.
Tu pourrais présenter l'ensemble sous la forme d'un tableau.
Pas de vérification à faire pour x=−7x = -7x=−7 et x=14x=\dfrac{1}{4}x=41.
-
Sakura kikuchi dernière édition par Sakura kikuchi

Bonsoir @Noemi mervi pour ta correction je vais rectifier mes erreurs
Mais enfaite pourquoi je dois pas faire de vérification ???
Mon problème c'est que je ne sais pas quant il faut en faire une ou pas ..
-
Une remarque : Ecrit un titre plus court et note tes attendus et questions avec l'énoncé de l'exercice.
Ceux sont les valeurs frontières des domaines donc pas de vérification.
Un graphique pour vérification éventuelle. Les abscisses des points A et B sont les solutions.
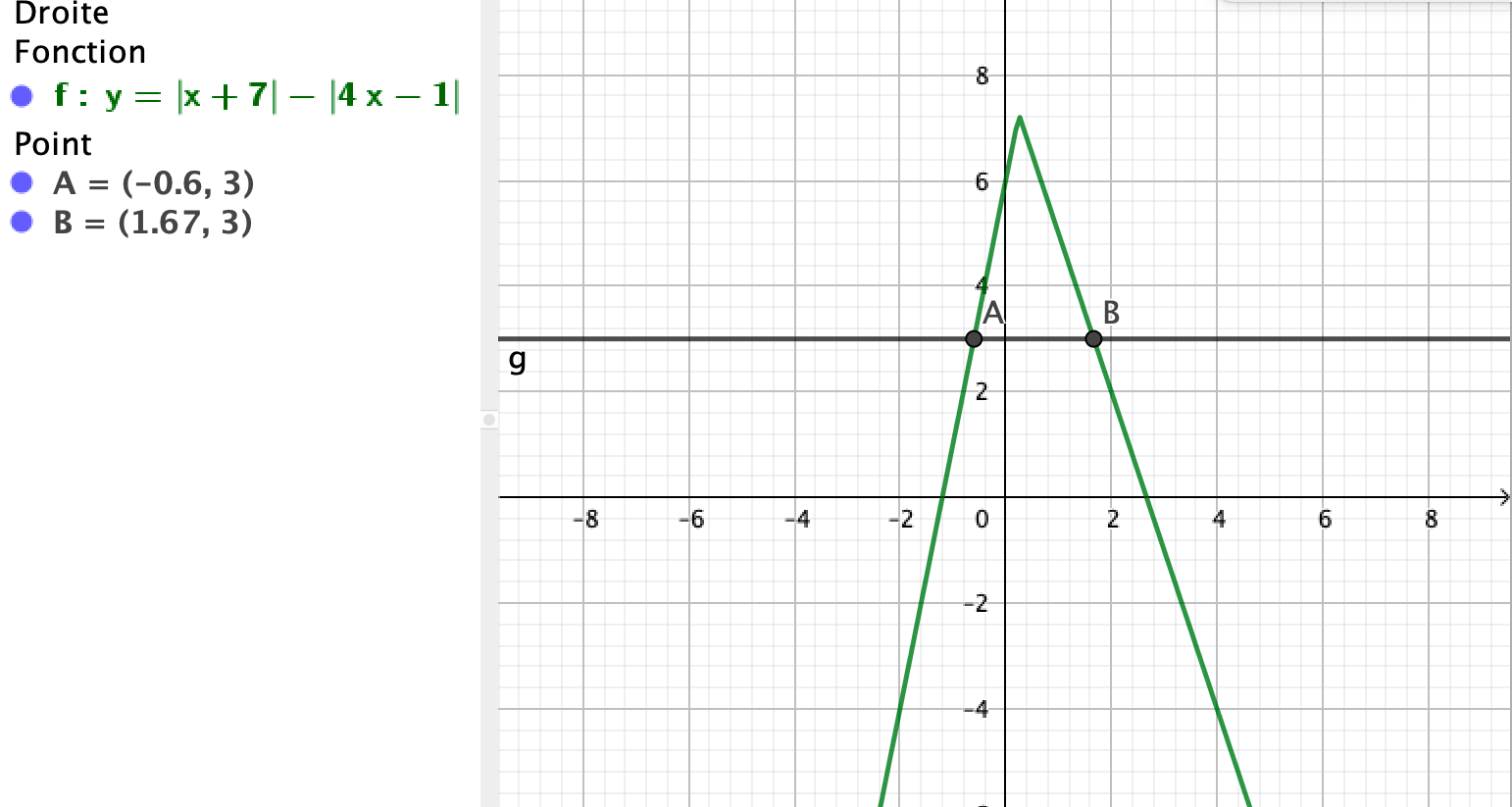
-
mtschoon dernière édition par mtschoon

Bonjour,
@Sakura-kikuchi ,@Noemi t'a indiqué pourquoi tu n'as pas de vérification à faire pour x=−7x=-7x=−7 et x=14x=\dfrac{1}{4}x=41
Je te donne ma démarche personnelle.
Tu dois résoudre l'équation pour tout x de R c'est à dire pour x∈]−∞,+∞[x\in ]-\infty,+\infty[x∈]−∞,+∞[ car l'ensemble de définition de la fonction f définie par f(x)=|x+7|-|4x-1| est R.
Lorsqu'on regarde ce que tu as fait, tu as travaillé pour
x∈]−∞,−7[∪ ]−7,14[ ∪ ]14,+∞[x\in \biggr]-\infty, -7\biggr [\cup\ \biggr]-7,\dfrac{1}{4}\biggr[\ \cup\ \biggr]\dfrac{1}{4},+\infty\biggr[x∈]−∞,−7[∪ ]−7,41[ ∪ ]41,+∞[
(les crochets sont ouverts)
Pour compléter rigoureusement l'étude sur tout R , tu étudies le cas x=−7x=-7x=−7 et le cas x=14x=\dfrac{1}{4}x=41Pour x=−7x=-7x=−7, ∣x+7∣−∣4x−1∣=−29|x+7|-|4x-1|=-29∣x+7∣−∣4x−1∣=−29
−29≠3-29\ne 3−29=3 donc −7-7−7 n'est pas solution.Pour x=14x=\dfrac{1}{4}x=41, ∣x+7∣−∣4x−1∣=294|x+7|-|4x-1|=\dfrac{29}{4}∣x+7∣−∣4x−1∣=429
294≠3\dfrac{29}{4}\ne 3429=3 donc 294\dfrac{29}{4}429 n'est pas solution.L'ensemble S des solutions est donc :
S={−35,53}S=\biggr\lbrace{-\dfrac{3}{5},\dfrac{5}{3}\biggr\rbrace}S={−53,35}
-
mtschoon dernière édition par mtschoon

@Sakura-kikuchi , je te joins un schéma donnant une vision globale de l'étude.
La représentation de f est la ligne "brisée" continue composée des 3 parties (bleue, rouge, verte) correspondant à tes 3 cas étudiés. du point C d'abscisse −7-7−7 et du point D d'abscisse 14\dfrac{1}{4}41
La droite d'équation y=3 est en noire.
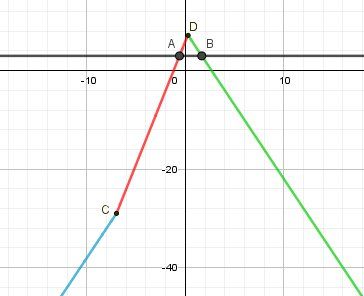
Bonne réflexion.
-
Sakura kikuchi dernière édition par

@mtschoon merci beaucoup
-
Sakura kikuchi dernière édition par

@Noemi d'accord
Oki merci bcp
-
mtschoon dernière édition par mtschoon

@Sakura-kikuchi , de rien !
Nous faisons au mieux...J'espère que tu as tout compris.