Fonction avec ln ; point fixe
-
Wil Fried dernière édition par Noemi

Bonjour, je demande de l'aide.
On donne f(x)= (1/2)x-ln(x)
1-Variation de f et tracer son graphe ( ce que j'ai pu faire )
J'ai obtenu que f est décroissante sur ]0;2] et croissante sur [2;+00[
2-Montrer que f admet un unique point fixe
Aidez moi pour la deuxième question. Je la croise dans plusieurs exercices, mais je ne sais pas comment la traiter. Peut-être dois je faire f(x)=x ?
Par ailleurs, avoir l'explication du théorème des valeurs intermédiaires car paraît-il qu'ils sont liés.
Merci, bonne journée à vous.
-
mtschoon dernière édition par mtschoon

@Wil-Fried , bonjour,
Oui pour la question 1
Pour la question 2, tu dois prouver que l'équation f(x)=xf(x)=xf(x)=x a une solution unique, que je note α\alphaα
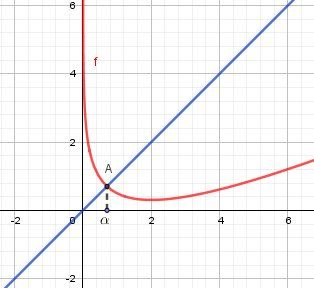
Graphiquement, α\alphaα est l'abscisse du point d'intersection de la représentation graphique de f avec la droite d'équation y=x
Piste pour la démonstration,
Soit g(x)=f(x)−x=−x2−ln(x)g(x)=f(x)-x=-\dfrac{x}{2}-ln(x)g(x)=f(x)−x=−2x−ln(x)
Tu étudies les variation de g sur ]0,+∞[]0,+\infty[]0,+∞[
Tu dois trouver que g est dérivable (donc continue) et strictement décroissante .
limx→0+g(x)=+∞\displaystyle \lim_{x\to 0^+} g(x)=+\inftyx→0+limg(x)=+∞
limx→+∞g(x)=−∞\displaystyle \lim_{x\to +\infty} g(x)=-\inftyx→+∞limg(x)=−∞Lorsque tu auras fait cela , tu pourras utiliser le théorème des valeurs intermédiaires (cas de la bijection) pour prouver l'existence et l'unicité de la valeur α\alphaα :
g est continue et strictement décroissante de ]0,+∞[]0,+\infty[]0,+∞[ vers R, donc bijective.
0 a donc un antécédent unique α\alphaα par g, c'est à dire il existe une seule valeur unique α\alphaα de ]0,+∞[]0,+\infty[]0,+∞[ telle que g(α)=0g(\alpha)=0g(α)=0 , c'est à dire telle que f(α)=αf(\alpha)=\alphaf(α)=αTu peux trouver une valeur approchée de α\alphaα à la calculatrice.
Sauf erreur, 0.7<α<0.80.7\lt \alpha \lt 0.80.7<α<0.8Regarde tout ça de près et reposte si besoin.
-
mtschoon dernière édition par mtschoon

Représentation graphique de f avec la droite d'équation y=x
Représentation graphique de g
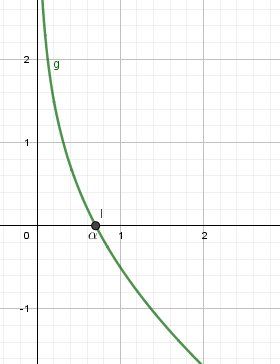
-
mtschoon dernière édition par

@Wil-Fried ,
Je viens de voir que tu a mis ta question dans la rubrique "Supérieur".
Cela correspond au programme de Terminale.
Peut-être que la modération la déplacera.
-
Wil Fried dernière édition par

@mtschoon Merci beaucoup!
-
Wil Fried dernière édition par Wil Fried

@mtschoon comment utiliser le théorème des valeurs intermédiaires pour prouver l'existence et l'unicité de la valeur alpha comme vous lavez dis ??
-
mtschoon dernière édition par mtschoon

@Wil-Fried , il faut que tu regardes ce que te dit ton cours sur le théorème des valeurs intermédiaires.
Je t'explicite un peu ce théorème , dans la version utile à ton exercice :
g est continue et strictement monotone sur un intervalle I dont l'image par g est J, donc tout élément β\betaβ de J a un antécédent unique α\alphaα dans I, c'est à dire :
il existe un élément unique α\alpha α de I tel que g(α)=βg(\alpha)=\betag(α)=βDans ton exercice :
I=]0,+∞[I=]0,+\infty[I=]0,+∞[
J=R=]−∞,+∞[J=R=]-\infty,+\infty[J=R=]−∞,+∞[
β=0\beta=0β=0
α\alphaα est l'élément unique tel que g(α)=0g(\alpha)=0g(α)=0Bonne réflexion.
-
mtschoon dernière édition par

Merci Noemi d'avoir déplacer ce topic en "Terminale"
-
mtschoon dernière édition par mtschoon

@Wil-Fried , bonjour,
Si tu veux un cours approfondi sur le TVI, tu peux regarder ici :
http://maths.desfontaines.free.fr/IMG/pdf/Quand_et_comment_utiliser_le_theoreme_des_valeurs.pdfBon approfondissement.
-
Wil Fried dernière édition par

@mtschoon Ohh merciii


-
mtschoon dernière édition par

@Wil-Fried , de rien !
C'est bien de répondre.
Contente que l'aide te soit utile.