probabilité conditionnelle

Bonjour vous pouvez m'aidez svp

Une histoire de Noël ..ou presque

Sur la table du salon de la famille Crépon, en ce soir de réveillon, trône une grosse

boîte de chocolats :

• 35% de ceux-ci sont enrobés de chocolat noir, les autres de chocolat au lait,
• 30% des chocolats noirs de la boite sont fourrés avec une crème qui contient de

l'alcool alors que seulement 10% des chocolats au lait sont alcoolisés.
Pendant que ses parents sont occupés à accueillir les invités, Archibald Crépon qui est un polisson", s'approche de la table et, sans regarder, pioche au hasard un chocolat qu'il s'empresse de croquer. Hélas, le voila bien puni! car aussitôt la première bouchée avalée, il se met à pleurnicher let crier: "c'est pas bon, c'est pas bon". Il avait pris un chocolat alcoolisé!

Quelle est la probabilité que le chocolat subtilisé par ce gourmand d'Archibald soit un

chocolat au lait? (on donnera le résultat sous forme de fraction irréductible). On attend évidemment, des évènements clairement définis éventuellement, un arbre pondéré EXPLICATIONS

Bonnes fêtes

Bonsoir pouvens,

As tu fait un arbre pondéré ?

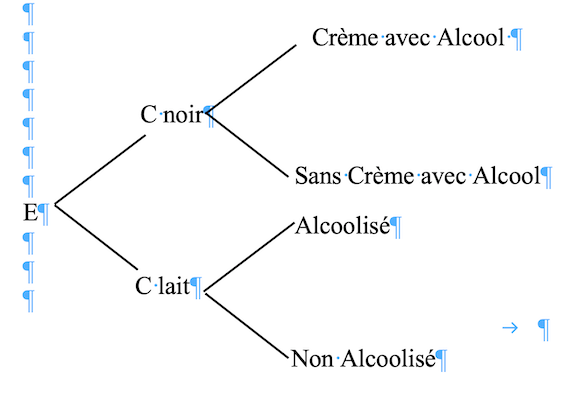
Complète l'arbre avec les probabilités.
Indique tes éléments de réponse.

Bonnes fêtes.

@Noemi ~~

Chocolat noir 0.35 . Noir alcool 0.30 . Non alcool 0.70
Chocolat lait 0,65 . Au lait alcool 0.10. Au lait non alcoolisé 0.90

Oui j avais déjà fait l'arbre pondéré mais du coup sur l arbre j ai déjà la probabilité des chocolat au lait

Bonjour,

@pouvens , je regarde ta réponse.
Oui , les probabilités que tu indiques sont bonnes (pour l'arbre)

Relis bien la question :
On demande la probabilité qu' Archibald ait pris un chocolat au lait sachant que ce chocolat est alcoolisé.
C'est une probabilité conditionnelle dont il s'agit.

Il faut, avec les valeurs de l'arbre, calculer d'abord la probabilité $p (A)$ pour qu'un chocolat soit alcoolisé.

Ensuite, il faut calculer :
$pA(Clait)=p(Clait∩A)p(A)p_A(C_{lait})=\dfrac{p(C_{lait} \cap A)}{p(A)}$

Tiens nous au courant de tes calculs si tu as besoin.

D'accord merci , J'ai trouvé environ 0,38

@pouvens

C'est correct.

Bonjour,

@pouvens ,

ma calculette me donne exactement $1334\dfrac {13}{34}$

0.38 en est une valeur approchée.