Étude de variation de f
-
Wil Fried dernière édition par Wil Fried

Salut! J'ai une autre préoccupation svp!
Il s'agit d'étudier les variations de la fonction suivante
ln(x+1)x\frac{ln(x+1)}{x}xln(x+1)
J'ai d'abord déterminé DfDfDf et j'ai trouvé ]−1;0[U]0;+∞[]-1;0[U]0;+\infty[]−1;0[U]0;+∞[
J'ai ensuite dérivé et j'ai trouvé
x−(x+1)ln(x+1)x2(x+1)\frac{x-(x+1)ln(x+1)}{x^2(x+1)}x2(x+1)x−(x+1)ln(x+1)
Mon problème est que je sais pas comment étudier le signe de la dérivée,néanmoins j'ai constaté que le dénominateur est strictement positif sur DfDfDf
-
Bonjour Wil-Fried,
Etudie les variations de la fonction ggg : g(x)=x−(x+1)ln(x+1)g(x) = x-(x+1)ln(x+1)g(x)=x−(x+1)ln(x+1) .
-
Wil Fried dernière édition par

Bonsoir @Noemi, Quel est donc le lien entre les variations de la nouvelle fonction ggg et le signe de la dérivée de fff ?
-
Le domaine de variation de la fonction ggg va te permettre dans déduire le signe de la dérivée.
Wil Fried, tu postes en terminale S et en Supérieur. En quelle classe es-Tu ?
-
mtschoon dernière édition par mtschoon

Bonjour,
@Wil-Fried , j'explicite un peu le raisonnement si tu as besoin,
g(x)=x−(x+1)ln(x+1)g(x)=x-(x+1)ln(x+1)g(x)=x−(x+1)ln(x+1)
g est définie, dérivable sur ]−1,+∞[]-1,+\infty[]−1,+∞[
En étudiant les variations de g , tu dois trouver que son maximum est pour x=0x=0x=0 et que g(0)=0g(0)=0g(0)=0Conséquence : pour x∈]−1,0[∪]0,+∞[x\in ]-1,0[ \cup ]0,+\infty[x∈]−1,0[∪]0,+∞[, g(x)<0g(x)\lt 0g(x)<0
f′(x)=g(x)x2(x+1)f'(x)=\dfrac{g(x)}{x^2(x+1)}f′(x)=x2(x+1)g(x)
Tu as déjà "constaté" que le dénominateur de f′(x)f'(x)f′(x) est strictement positif sur le domaine
Tu peux donc déduire le signe de f′(x)f'(x)f′(x) puis le sens de variation de fffIndique nous si ces détails te suffisent et n'oublie pas de répondre à la question de Noemi : en quelle classe es-tu ?
-
Wil Fried dernière édition par

Bonjour @Noemi !
Je suis Wilfried, étudiant en 1ère année d'économie dans une université de la Côte d'ivoire. Je prépare par ailleurs un concours d'entrée dans une école de statistique et d'économie appliquée ( ENSEA ). Et vu que les sujets que je traite portent souvent sur le Supérieur, souvent aussi sur la terminale S voilà pourquoi je poste ainsi. Veuillez donc me dire comment poster si ma manière n'est pas la bonne.
-
Wil Fried dernière édition par

Merci beaucoup @mtschoon et bonjour!
Je comprend mieux
Je vous ai répondu vous et @Noemi concernant mon niveau.
-
mtschoon dernière édition par mtschoon

Re-bonjour @Wil-Fried ,
Merci pour ton explication relative à ton niveau.
C'est clair maintenant et pour moi, ta méthode est bonne (SUP ou TS suivant le cas)
L'exercice que tu poses ici est bien de niveau Terminale.
Noemi te donnera certainement son avis.Pour l'exercice de ce topic, fais le en entier et dis nous si tu as des difficultés (je détaillerai plus) ou si tout va.
Bon travail !
-
Wil Fried dernière édition par Wil Fried

@mtschoon Je ne trouve pas le même résultat que vous.
g′(x)=−ln(x+1)g'(x)=-ln(x+1)g′(x)=−ln(x+1)
Je trouve que pour x∈]−1;e−1[x\in]-1;e-1[x∈]−1;e−1[ g′(x)>0g'(x)\gt0g′(x)>0 et ∀x∈]e−1;+∞[\forall x\in]e-1;+\infty[∀x∈]e−1;+∞[ g'(x)<0$
Donc mon maximum est e−1e-1e−1 et il ne me permet pas de déduire le signe de g(x)g(x)g(x)
-
Wil Fried dernière édition par

@mtschoon Désolé, j'ai fais une erreur lors de mes calculs
 .. je rectifie
.. je rectifie

 ️
️

 ️
️
-
mtschoon dernière édition par

@Wil-Fried , je regarde,
−ln(x+1)=0-ln(x+1)=0−ln(x+1)=0 <=> ln(x+1)=0ln(x+1)=0ln(x+1)=0 <=>x+1=1x+1=1x+1=1 <=>x=0x=0x=0
Il te reste à faire le cas −ln(x+1)>0-ln(x+1)\gt 0−ln(x+1)>0 et le cas −ln(x+1)<0-ln(x+1)\lt 0−ln(x+1)<0
-
Wil Fried dernière édition par Noemi

@mtschoon J'ai fais directement −ln(x+1)≥0-ln(x+1)\ge0−ln(x+1)≥0
⟹ \implies⟹ln(x+1)≤0ln(x+1)\leq0ln(x+1)≤0
⟹ \implies⟹x+1≤1x+1\leq1x+1≤1
⟹ \implies⟹x≤0x\leq0x≤0
Du coup j'ai la valeur qui annule l'inéquation et en même temps l'intervalle sur lequel −ln(x+1)-ln(x+1)−ln(x+1) est positif, c'est-à-dire sur ]−1;0[]-1;0[]−1;0[ et j'en déduis qu'il est négatif sur ]0;+∞[]0;+\infty[]0;+∞[ et le maximum est 000
-
Wil Fried dernière édition par

@mtschoon Svp pourquoi est ce que la partie en rouge n'est pas apparue comme je le voulais ? J'ai respecté la ReˋgleRègleReˋgle pourtant

-
mtschoon dernière édition par mtschoon

@Wil-Fried ,c'est le symbole \gq qui n'est pas reconnu
$ -\ln(x+1)\ge 0$ sans espace donne : −ln(x+1)≥0-\ln(x+1)\ge 0−ln(x+1)≥0
C'est bon pour le signe de g'(x).
Tu peux continuer de traiter l'exercice.
Reposte si besoin.
-
mtschoon dernière édition par mtschoon

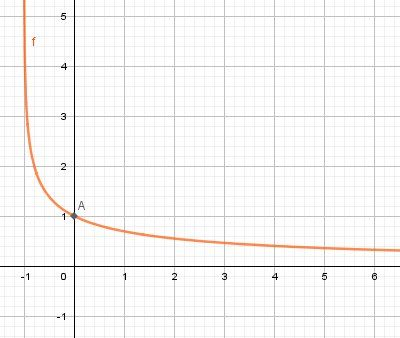
@Wil-Fried , pour vérifier le sens de variation de la fonction f que tu as dû trouver, je te mets la représentation graphique de f (le point A ne fait pas partie de la représentation graphique de f)
Remarque : le point A correspond au prolongement de f par continuité en 0, mais ce n'est pas demandé dans ton exercice.
-
Wil Fried dernière édition par

@mtschoon Merciii
-
mtschoon dernière édition par

De rien @Wil-Fried et bon dimanche !