Les variations d'une fonction
-
Prince Of Darkness dernière édition par Noemi
Bonjour,
Je dois trouver les variation de la fonction f(x)= -4*(racine carre de x)-3x+4
J'ai trouve que f'(x)= -4*(1/2(racine carre de x) )-3Je bloque ici car je n'arrive pas a trouver une methode pour trouver les racines de cette fonction derivee.
-
@Prince-Of-Darkness Bonsoir,
f′(x)=−2x−3=−2+3xxf'(x)= -\dfrac{2}{\sqrt x}-3 = -\dfrac{2+3\sqrt x}{\sqrt x}f′(x)=−x2−3=−x2+3x
Etudie le signe de la dérivée pour xxx strictement positif.
-
mtschoon dernière édition par mtschoon

Bonjour,
Quelque précisions, si besoin, @Prince-Of-Darkness
Pour x>0\boxed{x\gt 0}x>0 , f est définie et dérivable.
la dérivée de xxx-> x\sqrt xx est xxx-> 12x\dfrac{1}{2\sqrt x }2x1 d'où
f′(x)=−4(12x)−3=−2(1x)−3f'(x)=-4(\dfrac{1}{2\sqrt x })-3=-2(\dfrac{1}{\sqrt x })-3f′(x)=−4(2x1)−3=−2(x1)−3En réduisant au même dénominateur x\sqrt xx, comme te l'a indiqué Noemi, on peut écrire :
f′(x)=−2+xxf'(x)=-\dfrac{2+\sqrt x}{\sqrt x}f′(x)=−x2+xPour x>0x\gt 0x>0, x>0\sqrt x\gt 0x>0,
donc 2+x>02+\sqrt x\gt 02+x>0
donc 2+xx>0\dfrac{2+\sqrt x}{\sqrt x} \gt 0 x2+x>0
donc f′(x)<0f'(x)\lt 0f′(x)<0
donc f strictement décroissante.
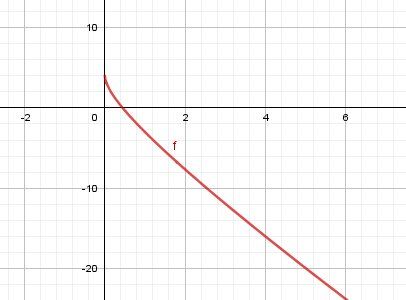
Bon travail.