Exercice sur Produit scalaire et ligne de niveau

Bonjour vous pouvez m'aider avec cette partie plz shuii un peu coincé avec la question 4
Soit ABC un triangle équilatéral de côté 4cm et G son centre de gravité. I est le milieu de [AB] et D le point vérifiant: BD.BC

calcluler BA.BC
Quelle est la nature du quadrilatère ABCD
determiner et construire l'ensemble des points M du plan tels que: MA.MC=5
4.a) Montrer que pour tout point M du plan on a : MA.MC- $MB^2$ = MB.BD+8
b.) En déduire l'ensemble (V) des points M du plan tels que MA.MC- $MB^2$ -8=0
....
NB les points (.) Signifient scalaire

@arona-Tounkara Bonjour,

Vérifie l'énoncé et complété la relation : $B D . B C = ? ? ?$

@arona-Tounkara
J'ai fait une erreur en écrivant
D le point vérifiant BD=2BI

@arona-Tounkara

Ce n'est pas plutôt vecteur CD = 2 vecteur BI. ?

@Noemi
Non c'est bien vecteur BD = 2 vecteurs BI

@arona-Tounkara

Donc l'erreur est peut-être I milieu de [AC] ?

@Noemi
D'après l'énoncé I est le milieu de [AB]
J'ai vérifié; il n'y a aucune erreur

@arona-Tounkara

Tu as fait une figure ?

Quelle est la nature du quadrilatère $A B C D$ ?

Bonjour,

Que de fautes dans cet énoncé !

Pour que les questions posées soient possibles , J'ai pris I milieu de [AC] et D le point vérifiant $AD→=BC→\overrightarrow{AD}=\overrightarrow{BC}$

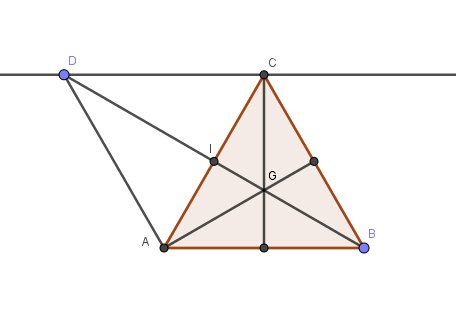
parallélogramme.jpg

@arona-Tounkara , quelques pistes pour démarrer,

ABCD est un parallélogramme de centre I

$MA→.MC→=5\overrightarrow{MA}.\overrightarrow{MC}=5$
c'est à dire
$(MI→+IA→)((MI→+IC→)=5(\overrightarrow{MI}+\overrightarrow{IA})((\overrightarrow{MI}+\overrightarrow{IC})=5$
$(MI→+IA→)((MI→−IA→)=5(\overrightarrow{MI}+\overrightarrow{IA})((\overrightarrow{MI}-\overrightarrow{IA})=5$
$MI→2−IA→2=5\overrightarrow{MI}^2-\overrightarrow{IA}^2=5$

$MI^2-IA^2=5$
$MI^2-4=5$
$MI^2=9$
$MI=3\boxed{MI=3}$

Tu tires la conclusion sur l'ensemble des points M.

Essaie de poursuivre et tiens nous au courant si besoin.

Bonjour,

On retrouve cet énoncé (ou presque) sur le net, par exemple ici : file:///C:/Users/Util/Downloads/Devoir%20Corrig%C3%A9%20de%20Contr%C3%B4le%20N%C2%B01%20-%20Math%20-%20g%C3%A9n%C3%A9ralit%C3%A9s%20sur%20les%20fonctions-continuit%C3%A9-limites-produit%20scalaire%20-%203%C3%A8me%20Math%C3%A9matiques%20(2015-2016)%20Mr%20Mhamdi%20Abderrazek%20(1).pdf

Voir l'exercice n°4

Il y a un "détail" qui change c'est que la donnée sur le point I est remplacée par "I = A * C" ... Ce qui est tout à fait incohérent.

On ne peux que déplorer le manque de sérieux de beaucoup exercices proposés, qui sont bourrés d'erreurs et presque jamais remis correct par beaucoup de profs.

Je ne sais pas où on va ... mais on y va très vite.

@arona-Tounkara , re-bonjour,

@arona-Tounkara , je regarde la suite pour m'assurer que les modifications proposées conviennent bien à la question 4)a) ; çà a l'air d'être le cas.

Prouver que :
$MA→.MC→−MB2=MB→.BD→+8\boxed{\overrightarrow{MA}.\overrightarrow{MC}-MB^2=\overrightarrow{MB}.\overrightarrow{BD}+8}$

Calcul :
$MA→.MC→=MI2−4\overrightarrow{MA}.\overrightarrow{MC}=MI^2-4$ d'après le calcul fait à la question précédente.
donc :
$MA→.MC→−MB2=MI2−4−MB2\overrightarrow{MA}.\overrightarrow{MC}-MB^2=\boxed{MI^2-4-MB^2}$

Comme à la question précédente, vu que I est aussi le milieu de [BD], en faisant le même type de calcul, tu dois trouver :
$MB→.MD→=MI2−IB2\overrightarrow{MB}.\overrightarrow{MD}=MI^2-IB^2$
Reste à calculer la valeur numérique de $I B$
En utilisant le théorème de Pythagore dans le triangle AIB rectangle en I, après calcul, tu dois trouver
$IB^2=12$

d'où

$MB→.BD→=MB→.(BM→+MD→)=MB→.BM→+MB→.MD→\overrightarrow{MB}.\overrightarrow{BD}=\overrightarrow{MB}.(\overrightarrow{BM}+\overrightarrow{MD})=\overrightarrow{MB}.\overrightarrow{BM}+\overrightarrow{MB}.\overrightarrow{MD}$

$MB→.BD→=−MB2+MI2−12\overrightarrow{MB}.\overrightarrow{BD}=-MB^2+MI^2-12$
$MB→.BD→+8=−MB2+MI2−4\overrightarrow{MB}.\overrightarrow{BD}+8=\boxed{-MB^2+MI^2-4}$

L'égalité proposée à la question 4)a) est donc exacte.

Regarde cette question de près et fais la 4)b) qui en est la déduction.

Propose tes réponses si tu as besoin d'une vérification.