Maths (probabilités conditionnelles et indépendance)

Bonjour j'aurais besoin d'aide pour cette exercice svp :
Import random
a = random.randint(1,5)
if a == 1:
b = random.randint(1,3)
if b == 1:
print("Rouge")
else:
print("Orange")
else :
b = random.randint(1,12)
if b > 8:
print("Rouge")
else:
print("Orange")
Les événements « a=1 » et « Le programme affiche Rouge »
sont-ils indépendants ?

@Paredes-mayra Bonjour,

Cherche dans quels cas, le programme affiche "Rouge".

Bonjour,

@Paredes-mayra , comme te le dit Noemi, il faut que tu cherches la probabilité pour que le programme affiche "Rouge"
Bien sûr, il faut que tu cherches aussi la probabilité pour que "a=1" et aussi la probabilité pour que "a=1" et que le programme affiche "Rouge".

Je pense que faire un arbre probabiliste est le plus simple pour répondre à ces questions et tirer la conclusion.

@Paredes-mayra , re-bonjour,

Si tu souhaites faire une arbre probabiliste, tu peux compléter celui-ci , avec les probabilités sur les branches.
L'évènement "a=1" a pour probabilité $15\dfrac{1}{5}$ vu que a prend 5 valeurs possibles {1,2,3,4,5}
En conséquence, l'évènement "non a=1" a pour probabilité $1−15=451-\dfrac{1}{5}=\dfrac{4}{5}$ .
R est l'évènement "le programme affiche Rouge"
O est l'évènement "le programme affiche Orange"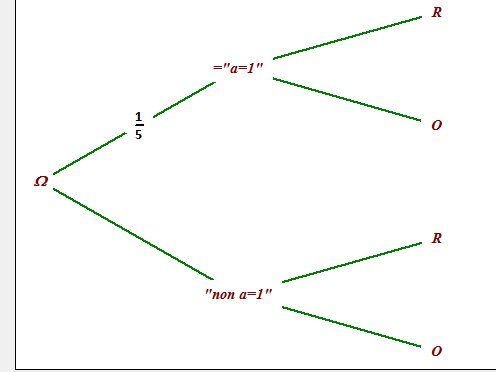

Tiens nous au courant de tes réponses si tu as besoin d'aide ou vérification.

Bonjour,

@Paredes-mayra a dû terminer seul son exercice qu'il date d'une semaine.

Quelques pistes pour consultation éventuelle

En complétant l'arbre, on doit trouver , après calculs :

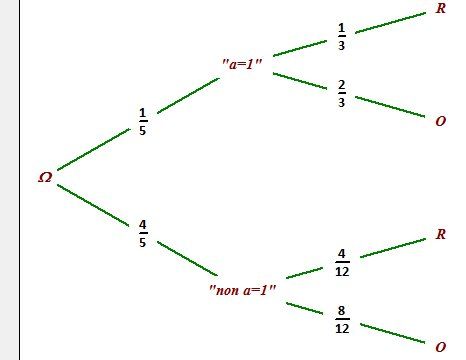
En faisant les calculs avec l'arbre :

$p(a=1)=15p(a=1)=\dfrac{1}{5}$
$p(R)=(15×13)+(45×412)=13p(R)=(\dfrac{1}{5}\times \dfrac{1}{3})+(\dfrac{4}{5}\times \dfrac{4}{12})=\dfrac{1}{3}$
$p((a=1)∩R)=15×13=115p((a=1)\cap R)=\dfrac{1}{5}\times \dfrac{1}{3}=\dfrac{1}{15}$

Donc $p((a=1)∩R)=p(a=1)×p(R)\boxed{p((a=1)\cap R)=p(a=1)\times p(R)}$

On tire la conclusion.

Bons calculs éventuels.