résolution système population d'animaux

Bonjour

J'aurai une petite question par rapport à la résolution d'un système que j'ai déjà posté mais je n'arrive pas à retrouver le post. En tout cas, j'ai pas compris la correction de mon professeur

Voici, l'exercice :

On étudie l’évolution dans le temps d’une population animale. À la date n (en années), cette population se divise en xn jeunes et yn adultes. L’année comporte une saison hivernale et une saison de reproduction.
Lors de la saison hivernale, 40% des jeunes survivent et deviennent des adultes et 80% des adultes survivent.
Lors de la saison de reproduction, chaque adulte donne naissance à 2 jeunes (en fait 4 par femelle). Tous les adultes survivent.

Exprimez xn+1 et yn+1 en fonction de xn et yn. Ecrivez le système obtenu sous forme matricielle.
Je suis parvenue à écrire cela que
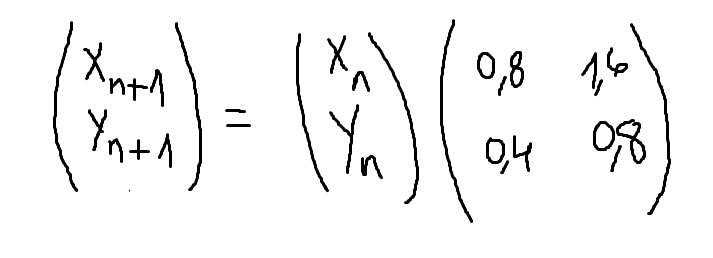
Calculez xn et yn en fonction de x0 et y0 du début de l’observation.

pour cette question là j'avais écris que :

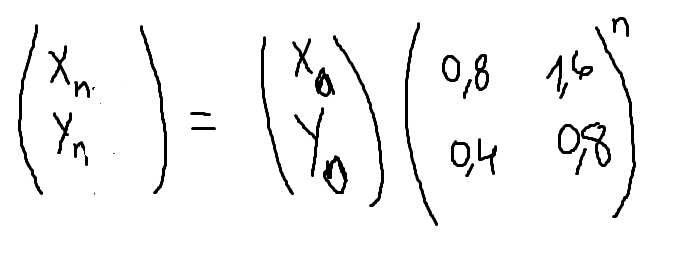
mais mon professeur a écris quelque chose en plus je ne sais pas d'ou ça vient :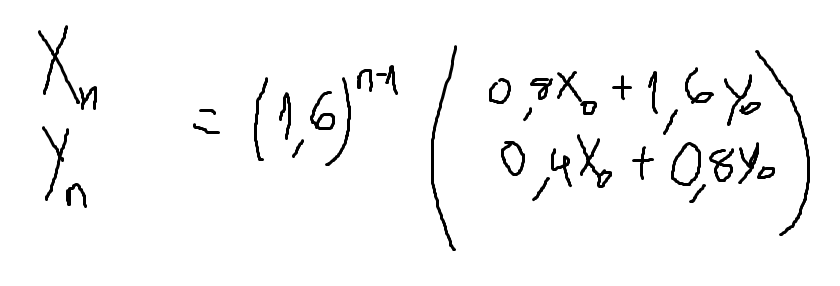

je vous remercie d'avance

@mimims Bonjour,

Exprime $X_2$ et $Y_2$ en fonction de $X_0$ et $Y_0$ .

Bonjour,

@mimims , une autre fois, je te conseille de reste sur ton topic initial si tu as besoin de compléments, pour que ce soit clair pour ceux qui viennent consulter
Ici : un exercice=un topic.

Dans un topic précédent, il a été démontré que :
$0.8)n×(X0Y0)\begin{pmatrix}X_n\cr Y_n\end{pmatrix}=\begin{pmatrix}0.8\ \ \ 1.6\cr 0.4\ \ \ 0.8\end{pmatrix}^n\times \begin{pmatrix}X_0\cr Y_0\end{pmatrix}$

( Remarque : lorsque tu écris le produit de deux matrices, fait attention à l'ordre car la multiplication matricielle n'est pas commutative)

Cela peut se décomposer en produit de trois matrices
$0.8)×(X0Y0)\begin{pmatrix}X_n\cr Y_n\end{pmatrix}=\begin{pmatrix}0.8\ \ \ 1.6\cr 0.4\ \ \ 0.8\end{pmatrix}^{n-1}\times \begin{pmatrix}0.8\ \ \ 1.6\cr 0.4\ \ \ 0.8\end{pmatrix}\times \begin{pmatrix}X_0\cr Y_0\end{pmatrix}$

Vu que la multiplication matricielle est associative, en faisant le produit des deux dernières matrices, on peut écrire :
$0.8)n−1×(0.8X0+1.6Y00.4X0+0.8Y0)\boxed{\begin{pmatrix}X_n\cr Y_n\end{pmatrix}=\begin{pmatrix}0.8\ \ \ 1.6\cr 0.4\ \ \ 0.8\end{pmatrix}^{n-1}\times \begin{pmatrix}0.8X_0+1.6Y_0\cr 0.4X_0+0.8Y_0\end{pmatrix}}$

Cette transformation est immédiate , mais ce n'est pas être l'écriture recherchée.

@mimims

Si tu exprimes $X_2$ et $Y_2$ en fonction de $X_0$ et $Y_0$

$0,8)×(X0Y0)\begin{pmatrix}X_2\cr Y_2\end{pmatrix}=\begin{pmatrix}0,8\ \ \ 1,6\cr 0,4\ \ \ 0,8\end{pmatrix}\times \begin{pmatrix}0,8\ \ \ 1,6\cr 0,4\ \ \ 0,8\end{pmatrix}\times \begin{pmatrix}X_0\cr Y_0\end{pmatrix}$
cela donne :
$1,28)×(X0Y0)\begin{pmatrix}X_2\cr Y_2\end{pmatrix}=\begin{pmatrix}1,28\ \ \ 2,56\cr 0,64\ \ \ 1,28\end{pmatrix}\times \begin{pmatrix}X_0\cr Y_0\end{pmatrix}$

Que l'on peut écrire :
$0,8)×(X0Y0)\begin{pmatrix}X_2\cr Y_2\end{pmatrix}=1,6\times \begin{pmatrix}0,8\ \ \ 1,6\cr 0,4\ \ \ 0,8\end{pmatrix}\times \begin{pmatrix}X_0\cr Y_0\end{pmatrix}$

d'ou
$0,8)×(X0Y0)\begin{pmatrix}X_n\cr Y_n\end{pmatrix}=(1,6)^{n-1}\times \begin{pmatrix}0,8\ \ \ 1,6\cr 0,4\ \ \ 0,8\end{pmatrix}\times \begin{pmatrix}X_0\cr Y_0\end{pmatrix}$

Re-bonjour,

La dernière propriété indiquée par @mimims est "évidente" pour n=1 et est démontrée par @Noemi , pour n=2.

Il reste à faire une démonstration par récurrence pour la prouver à un ordre n .

L'initialisation est faite en indiquant que la propriété est vraie pour n=1

Quelques pistes pour prouver l'hérédité,

On sait que :
$0.8)×(XnYn)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=\begin{pmatrix}0.8\ \ 1.6\cr 0.4\ \ 0.8\end{pmatrix}\times \begin{pmatrix}X_{n}\cr Y_{n}\end{pmatrix}$

Avec l'hypothèse de la récurrence :
$0.8)×(1.6)n−1×(0.8X0+1.6Y00.4X0+0.8Y0)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=\begin{pmatrix}0.8\ \ 1.6\cr 0.4\ \ 0.8\end{pmatrix}\times (1.6)^{n-1}\times \begin{pmatrix}0.8X_0+1.6Y_0\cr 0.4X_0+0.8Y_0\end{pmatrix}$
d'où :
$0.8)×(0.8X0+1.6Y00.4X0+0.8Y0)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=(1.6)^{n-1}\times \begin{pmatrix}0.8\ \ 1.6\cr 0.4\ \ 0.8\end{pmatrix}\times \begin{pmatrix}0.8X_0+1.6Y_0\cr 0.4X_0+0.8Y_0\end{pmatrix}$
Or,
$0.8)×(X0Y0)\begin{pmatrix}0.8X_0+0.6Y_0\cr 0.4X_0+0.8Y_0\end{pmatrix}=\begin{pmatrix}0.8\ \ 1.6\cr 0.4\ \ 0.8\end{pmatrix}\times \begin{pmatrix}X_{0}\cr Y_{0}\end{pmatrix}$

d'où
$0.8)×(X0Y0)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=(1.6)^{n-1}\ \begin{pmatrix}0.8\ \ 1.6\cr 0.4\ \ 0.8\end{pmatrix}\times \begin{pmatrix}0.8\ \ 1.6\cr 0.4\ \ 0.8\end{pmatrix}\times \begin{pmatrix}X_{0}\cr Y_{0}\end{pmatrix}$

En utilisant le calcul fait pour n=2
$1.28)×(X0Y0)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=(1.6)^{n-1}\times \begin{pmatrix}1.28\ \ 2.56\cr 0.64\ \ 1.28\end{pmatrix}\times \begin{pmatrix}X_{0}\cr Y_{0}\end{pmatrix}$

$0.8)×(X0Y0)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=(1.6)^{n-1}\times 1.6\times\begin{pmatrix}0.8\ \ 0.6\cr 0.4\ \ 0.8\end{pmatrix}\times \begin{pmatrix}X_{0}\cr Y_{0}\end{pmatrix}$

$0.8)×(X0Y0)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=(1.6)^{n}\times\begin{pmatrix}0.8\ \ 0.6\cr 0.4\ \ 0.8\end{pmatrix}\times \begin{pmatrix}X_{0}\cr Y_{0}\end{pmatrix}$

$(Xn+1Yn+1)=(1.6)n×(0.8X0+1.6Y00.4X0+0.8Y0)\begin{pmatrix}X_{n+1}\cr Y_{n+1}\end{pmatrix}=(1.6)^{n}\times\begin{pmatrix}0.8X_0+1.6Y_0\cr 0.4X_0+0.8Y_0\end{pmatrix}$

CQFD

(le professeur a gagné du temps en écrivant la propriété sans la démontrer.)