résolution d'un système

bonjour,

Je trouve un résultat très étrange à la question
Dans une cage, on a une population de 100 souris qui se compose de mâles gris et de femelles blanches. On laisse la population se développer pendant un mois. À la fin, on dénombre 284 souris.
L’accouplement de souris donne une fois sur quatre une souris blanche et trois fois sur quatre une souris grise. En un mois, le nombre de mâles x au début de l’expérience a été multiplié par 2 et le nombre de
femelles y au début de l’expérience a été multiplié par 3. Il n’y a pas eu de décès au cours de l’expérience.

Écrire le système linéaire permettant de déterminer le nombre de mâles et le nombre de femelles au
début de l’expérience, sous forme d’un système d’équations, puis sous sa forme matricielle.

a) Résoudre ce système en inversant la matrice associée.

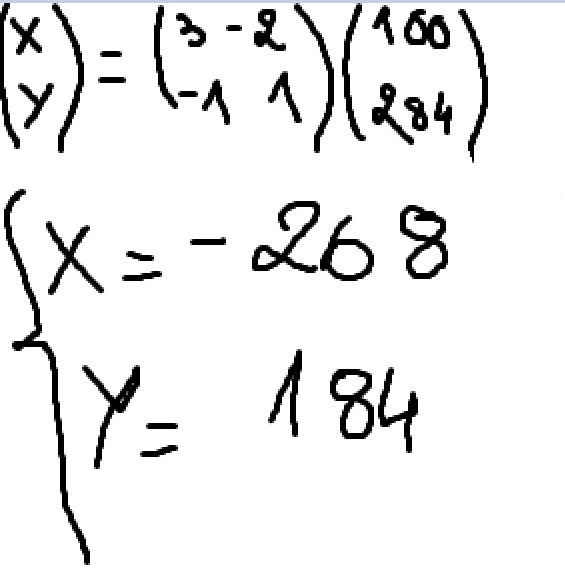
b) Déterminez le nombre de souris grises et de souris blanches à la fin du mois.
c) Que pouvez-vous en conclure ?
d) Retrouver le résultat par les méthodes de Cramer et du pivot de Gauss.

je vous remercie.

@mimims Bonjour,

Vérifie le système et la matrice inverse.

@Noemi

Bonjour, j'ai bien vérifié mais je ne vois pas ou est mon erreur.

@mimims

En prenant $x_0$ le nombre de mâles et $y_0$ le nombre de femelles.
Le système de départ est :
$x_0+y_0=100$
$2x_0+3y_0=284$

Vérifie la matrice inverse.

@Noemi, j'ai fait ça :

@mimims

C'est la matrice inverse qui est fausse pour la diagonale secondaire, on multiplie par -1, sans changer les valeurs.
La matrice est
3 ; -1
-2 ; 1.
$1)\begin{pmatrix} \ \ \ 3 \ -1 \cr -2 \ \ \ \ 1 \end{pmatrix}$

@Noemi
oui mais il faut faire la transposée par après non ?

@mimims

L'énoncé indique d'utiliser la matrice inverse.

@Noemi en fait ma comatrice est égale à ça et donc pour ma matrice inverse j'ai fait la transposée

@mimims

La comatrice est :

$1)\begin{pmatrix} \ \ \ 3 \ -2 \cr -1 \ \ \ \ 1 \end{pmatrix}$ .

@Noemi et pour trouver l'inverse d'une matrice on doit passer par la transposée ?

@Noemi après vérification, je trouve x=100 et y=184

@mimims

Vérifie les calculs, tu dois trouver $x_0=16$ et $y_0=84$ .
La somme doit faire 100.

$y0)\begin{pmatrix} \ x_0 \cr \ y_0 \end{pmatrix}$ = $1)\begin{pmatrix} \ \ \ 3 \ -1 \cr -2 \ \ \ \ 1 \end{pmatrix}$ . $284)\begin{pmatrix} \ 100 \cr \ 284 \end{pmatrix}$ .

Bonjour,

@mimims

Lorsque tu auras bien compris la méthode matricielle (évidemment, si tu as une calculette qui fait le calcul matriciel, en rentrant une matrice $M$ , c'est simple ; tu peut obtenir directement $M^{-1}$ puis le calcul du produit des matrices), ce qui te donne :

$1)×(100284)=(1684)\begin{pmatrix}\ \ \ \ 3\ \ \ -1\cr-2\ \ \ \ \ \ \ 1\end{pmatrix}\times \begin{pmatrix}100\cr 284\end{pmatrix}=\begin{pmatrix}16\cr 84\end{pmatrix}$

Pour vérifier, tu peux résoudre le système comme tu le faisais en classe de Troisième :
(ça se fait en deux lignes..., par substitution par exemple)

${x+y=1002x+3y=284\begin{cases}x+y=100\cr 2x+3y=284\end{cases}$

La première équation te donne : $y = 100 - x$
En substiuant dans la seconde :
$2 x + 3 (100 - x) = 284$ <=> $x=16\boxed{x=16}$
d'ou $y=100−16=84\boxed{y=100-16=84}$

Bons calculs.