Équations de premier degré

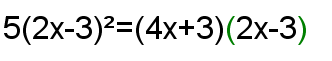
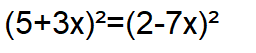
Bonjour, je n'arrive pas à résoudre ces deux équations. Es-ce que vous pourriez m'aider svp ? équa 1.PNG équa 2.PNG

@Laya-254 Bonjour,

Pour la première équation,
Ecris la sous la forme : $A (x) = 0$ puis tu factorises $(2 x - 3)$ .

Pour la deuxième équation,
Ecris la sous la forme = $A (x) = 0$ puis tu factorises en utilisant l'identité remarquable :
$a^2-b^2=(a-b)(a+b)$

Indique tes calculs et/ou résultats si tu souhaites une vérification.

Bonjour,

Le demandeur qui a posé la question n'est pas resté utilisateur longtemps...

Quelques compléments pour consultation éventuelle.

Pour la première équation.

$5(2x-3)^2-(4x+3)(2x-3)=0$
En mettant $(2 x + 3)$ en facteur
$(2 x - 3) [5 (2 x - 3) - (4 x + 3)] = 0$
Après calculs, on doit trouver
$(2 x - 3) (6 x - 18) = 0$
Solutions : $x=32x=\dfrac{3}{2}$ et $x = 3$

Pour la seconde équation

$5+3x)^2-(2-7x)^2=0$
En factorisant avec l'identité remarquable $a^2-b^2$
$[(5 + 3 x) + (2 - 7 x)] [(5 + 3 x) - (2 - 7 x)] = 0$
Après calculs, on doit trouver
$(7 - 4 x) (3 + 10 x) = 0$
Solutions : $x=74x=\dfrac{7}{4}$ et $x=−310x=-\dfrac{3}{10}$

Bons calculs.