variation de l'aire d'un rectangle

bonjour,
j'ai presque terminer mon dm, je suis bloqué a la question 3)b)
est-ce que vous pouvez m'aider svp.
merci d'avance!
voici l'énoncé
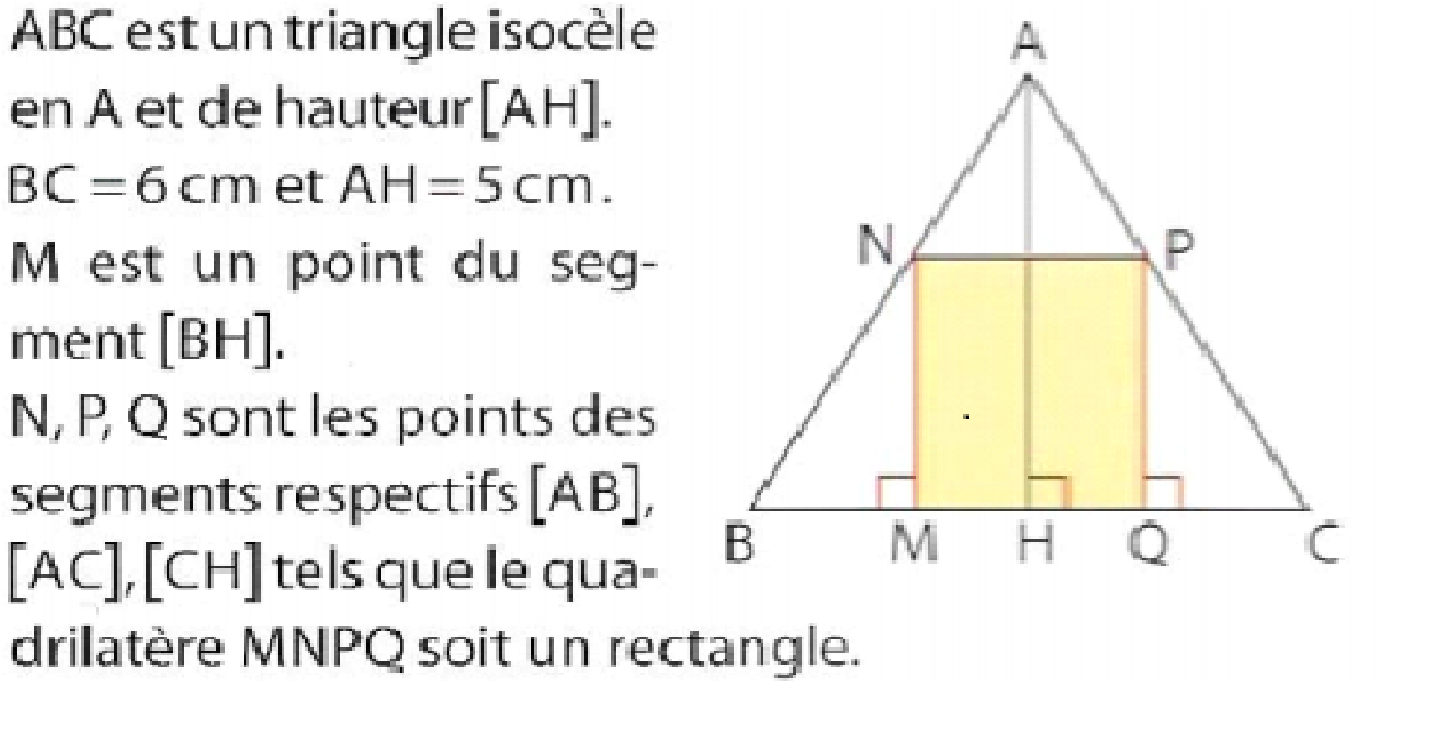
$dm math.png$
Le but de cet exercice est de déterminer la position du point M pour que l’aire de
ce rectangle soit maximale.
On note x la longueur BM.
On note f la fonction qui à x= BM (en cm) associe l’aire, en cm², du rectangle
MNPQ.

Donner, sans justifier, l’ensemble de définition D de f ? (autrement dit
donner l’intervalle D auquel appartient x ? )
a) Montrer que MN= 5/3 x
b) Exprimer MQ en fonction de x.
c) En déduire que l’aire f(x) du rectangle MNPQ est donnée par :
f(x)= 10x - 10/3 x²
a) Calculer f(3/2), puis vérifier que pour tout x de D :
f(x)−f(3/2)=-5/6 (2x-3)²

b) En déduire que f(3/2) est le maximum de f sur D

c) Quelles sont les dimensions du rectangle d’aire maximale ?

voici ce que j'ai fait.
$dm math.jpg$

Bonjour,

L'ensemble est correct.
Pour la question 3. b) que peut-on dire de $−56(2x−3)2-\dfrac{5}{6}(2x-3)^2$ ?

@Noemi on peut dire que c'est l'aire restant dans le triangle

Cette expression est négative ou nulle donc le maximum est atteint si elle est égale à 0, d'ou la valeur de $x$ à indiquer.

@Noemi j'ai pas trop bien compris

est-ce que je doit dire que f(2/3) est le maximum de f sur D car l'expression -5/6 (2x-3)² est négative. est-ce que j'ai bien compris

$f(x)−f(32)=−56(2x−3)2f(x)-f(\dfrac{3}{2})=-\dfrac{5}{6}(2x-3)^2$
soit :
$f(x)−f(32)≤0f(x)-f(\dfrac{3}{2})\leq0$
la valeur la plus grande que peut prendre:
$f(x)−f(32)f(x)-f(\dfrac{3}{2})$ est donc 0.
D'ou la conclusion .....

@Noemi ok merci, pouvez vous m'aider aussi pour la suite svp ;
comment je peut trouver les dimensions

Tu sais que $\dfrac{3}{2}$ . Calcule la valeur de MQ et de MN, puis l'aire du rectangle.

@Noemi j'ai trouver MQ=3 et MN=2,5

C'est juste.
Donc l'aire est égale à ....

@Noemi 7,5

Oui et n'oublie pas l'unité.

@Noemi est-ce que c'est correct

Pour la question b
il manque la conclusion
$f(x)−f(32)=0f(x)-f(\dfrac{3}{2})=0$
conduit à $\dfrac{3}{2}$ .

@Noemi ok merci beaucoup

@Noemi Pouvez-vous m'aider svp

@Joyca-Le-Boss Bonjour,

Tu demandes de l'aide pour quelle question ?

Bonjour,

Je pense que @Joyca-Le-Boss s'est seulement trompé de topic...

@mtschoon quel topic ?

Sauf erreur, @Joyca-Le-Boss , je pense que c'est sur celui-ci que tu travailles actuellement :
https://forum.mathforu.com/topic/31730/résous-le-système-par-la-méthode-de-gauss-pivot/7

Va voir, tu as de l'aide.

Bon travail.