Étant donnée la matrice A 2x2, détermine les matrices 2x2 qui commutent avec A.
-
Joyca Le Boss dernière édition par
Bonjour, Pouvez-vous m'aider à résoudre cet exercice svp. Merci d'avance pour votre aide.
A) Étant donnée la matrice A 2x2, détermine les matrices 2x2 qui commutent avec A.
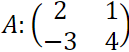
B) La matrice A de l’exercice précédent possède-t-elle une inverse ? Justifie et dans l’affirmative détermine celle-ci.
-
mtschoon dernière édition par

Re-bonjour @Joyca-Le-Boss ,
Je te mets quelques pistes ( je n'ai pas fait tous les calculs).
A) Tu cherches les matrices B de la forme (a bc d)\begin{pmatrix}a\ \ b \cr c\ \ d\end{pmatrix}(a bc d) telles que
A×B=B×AA\times B=B\times AA×B=B×ATu obtiens ainsi 4 équations, mais elles doivent se réduire à trois seulement.
Tu dois pouvoir calculer c et d en fonction de a et b.
Ainsi les matrices B seront exprimer en fonction de a et bB) A possède un inverse si et seulement si det(A)≠0det(A)\ne 0det(A)=0
det(A)=11det(A)=11det(A)=11 donc A inversibleA−1A^{-1}A−1 doit vérifier A×A−1=A−1×A=(1 00 1)A\times A^{-1}= A^{-1}\times A=\begin{pmatrix}1\ \ 0\cr 0\ \ 1\end{pmatrix}A×A−1=A−1×A=(1 00 1)
A−1A^{-1}A−1 fait partie de la famille B trouvée dans la question précédente
Tu utilises donc la réponse précédente pour trouver a et b tels que A×B=(1 00 1)A\times B=\begin{pmatrix}1\ \ 0\cr 0\ \ 1\end{pmatrix}A×B=(1 00 1)
Sauf erreur tu dois trouver ainsi que
B=A−1B=A^{-1}B=A−1=(411 −111311 211)\begin{pmatrix} \frac{4}{11}\ \ \frac{-1}{11}\cr \frac{3}{11}\ \ \frac{2}{11} \end{pmatrix}(114 11−1113 112)Bons calculs .
-
Joyca Le Boss dernière édition par
@mtschoon J'ai fait la A mais je sais pas si c'est juste , Pouvez-vous me montrer votre raisonnement svp ?
-
mtschoon dernière édition par

@Joyca-Le-Boss , bonjour,
Pour la question A), je t'ai déjà indiqué le principe, relis ma réponse.
A×B=B×AA\times B=B\times AA×B=B×AAprès calculs, en identifiant les coefficients respectifs des matrices A×BA\times BA×B et B×AB\times AB×A, tu obtiens 4 équations d'inconnues a,b,c,d.
Après transformations, sauf erreur, tu peux arriver à :
a+2b=da+2b=da+2b=d
c=−3bc=-3bc=−3bB=(a b−3b a+2b)B=\begin{pmatrix}a\ \ \ \ \ \ \ b\cr -3b\ \ a+2b\end{pmatrix}B=(a b−3b a+2b)
Tu peux utiliser cette expression de BBB pour la seconde question.
-
Joyca Le Boss dernière édition par
@mtschoon j'ai trouver c=−3b mais j'ai pas trouver a+2b=d comment avez-vous fait svp ? Pouvez-vous me donner un indice ?
-
mtschoon dernière édition par

J'ai obtenu d'abord
2a+c=2a−3b2a+c=2a-3b2a+c=2a−3b
−3a+4c=2c−3d-3a+4c=2c-3d−3a+4c=2c−3d
2b+d=a+4b2b+d=a+4b2b+d=a+4b
−3b+4d=c+4d-3b+4d=c+4d−3b+4d=c+4dEnsuite, j'ai transformé.
-
Joyca Le Boss dernière édition par
@mtschoon Vous avait transformé en isolant ou avec combinaison Linéaire?
-
Joyca Le Boss dernière édition par Joyca Le Boss
@mtschoon Comme résultat j'ai trouver a+2b=d
c=−3b
mais également : -3a + 3d = -2c Est-ce normal ?
-
mtschoon dernière édition par

Oui, c'est normal.
-
Joyca Le Boss dernière édition par
@mtschoon et donc je le note pas dans le resultat?
-
mtschoon dernière édition par

Comme je te l'ai suggéré, calcule a et b en fonction de c et d, ce qui te permettra de faire la seconde question sans difficulté.
-
Joyca Le Boss dernière édition par
@mtschoon donc je note directement le résultat qui est a+2b=d
c=−3b
-
mtschoon dernière édition par mtschoon

@Joyca-Le-Boss , je ne sais pas trop ce que tu veux dire par "résultat"
Tu donnes B sous la forme que je t'ai indiqué précédemment (les quatre termes en fonction de a et b)
-
Joyca Le Boss dernière édition par
@mtschoon ok je passe a la question b
-
Joyca Le Boss dernière édition par Joyca Le Boss
@mtschoon ensuite pour trouver l'inverse je dois trouver le det de A qui 11 et ensuite je dois multiplie la matrice A initial et la matrice B qu'on vient de trouver égale
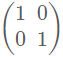
-
Joyca Le Boss dernière édition par
@mtschoon Est-ce correct comme raisonnement ?
-
mtschoon dernière édition par

Tout à fait.
-
Joyca Le Boss dernière édition par
@mtschoon et ensuite que faire svp ?
-
Joyca Le Boss dernière édition par
@mtschoon Est-ce correct svp ? car j'ai un doute

-
@Joyca-Le-Boss Bonjour,
Détermine aaa et bbb.
-
Joyca Le Boss dernière édition par
Ce message a été supprimé !
-
Joyca Le Boss dernière édition par
@Noemi si je fais ca c bon aussi ?

-
Tu écris A−1A^{-1}A−1 pour les deux matrices ?
La matrice du bas est correcte.
-
Joyca Le Boss dernière édition par
@Noemi Ah a la place je dois écrire B c'est ca ?
-
Joyca Le Boss dernière édition par
@Noemi Si j'écris comme ca c'est bon
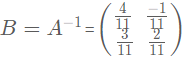
-
C'est correct.
-
Joyca Le Boss dernière édition par
@Noemi donc l'exercice est terminer ?
-
Oui, l'exercice est terminé.
Revois tout le raisonnement et l'aide qui t'a été apportée.
-
mtschoon dernière édition par
