Résous le système par la méthode de Gauss (pivot)
-
Joyca Le Boss dernière édition par
Bonjour, Pouvez-vous m'aider a résoudre cet exercice svp ?
Voici l'énoncé : Résous le système par la méthode de Gauss (pivot)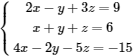
-
@Joyca-Le-Boss Bonjour,
Indique tes calculs et résultats.
-
Joyca Le Boss dernière édition par
Ce message a été supprimé !
-
Joyca Le Boss dernière édition par
@Noemi Est-ce correct ?

-
@Joyca-Le-Boss
La première étape est d'inverser la ligne 1 avec la ligne 2 pour obtenir un coefficient de 1 pour xxx pour la première ligne.
{x+y+z=62x−y+3z=94x−2y−5z=−15\begin{dcases} x+y+z=6 \cr 2x-y+3z=9 \cr 4x-2y-5z=-15 \end{dcases}⎩⎪⎪⎨⎪⎪⎧x+y+z=62x−y+3z=94x−2y−5z=−15
-
Joyca Le Boss dernière édition par
@Noemi et ensuite je fais quoi svp ?
-
{x+y+z=62x−y+3z=94x−2y−5z=−15\begin{dcases} x+y+z=6 \cr 2x-y+3z=9 \cr 4x-2y-5z=-15 \end{dcases}⎩⎪⎪⎨⎪⎪⎧x+y+z=62x−y+3z=94x−2y−5z=−15
Tu peux travailler avec les matrices :
(1 1 1 62 −1 3 9 4 −2 −5 −15)\begin{pmatrix} 1 \ \ \ \ \ \ 1 \ \ \ \ \ 1 \ \ \ \ \ 6\cr 2 \ \ -1 \ \ \ \ \ 3 \ \ \ \ \ 9\cr \ \ 4 \ -2\ -5\ -15 \end{pmatrix}⎝⎜⎛1 1 1 62 −1 3 9 4 −2 −5 −15⎠⎟⎞Puis :
(1 1 1 6 0 −3 1 −3 0 −6 −9 −39)\begin{pmatrix} 1 \ \ \ \ \ \ 1 \ \ \ \ \ 1 \ \ \ \ \ 6\cr \ 0 \ -3 \ \ \ \ \ 1 \ \ \ -3\cr \ \ 0 \ -6\ -9\ -39 \end{pmatrix}⎝⎜⎛1 1 1 6 0 −3 1 −3 0 −6 −9 −39⎠⎟⎞
-
Joyca Le Boss dernière édition par
@Noemi et j'ai trouver ca c'est juste ?

-
Joyca Le Boss dernière édition par
@Noemi ensuite j'ai divise par -3 la troisième L (L3) j'ai trouver 0 2 3 13 Voila
-
C'est correct mais sans le signe =.
Si tu n'arrives pas à écrire des matrices en direct
Tu peux écrire le résultat sous la forme
1 ; 1 ; 1 ; 6
0 ; 1; -1/3 ; 1
0 ; 2 ; 3 ; 13
-
Joyca Le Boss dernière édition par
@Noemi Pour la L2 j'ai laissé comme ca parce que je ne veux de fraction . ca ne change rien je pense et j'ai trouver ca

-
Tu dois avoir des 1 sur la diagonale de la matrice 3x3.
1 ; 1 ; 1 ; 6
0 ; 1; -1/3 ; 1
0 ; 0 ; 1 ; 3puis
1 ; 1 ; 0 ; 3
0 ; 1; 0 ; 2
0 ; 0 ; 1 ; 3Puis
....
-
Joyca Le Boss dernière édition par
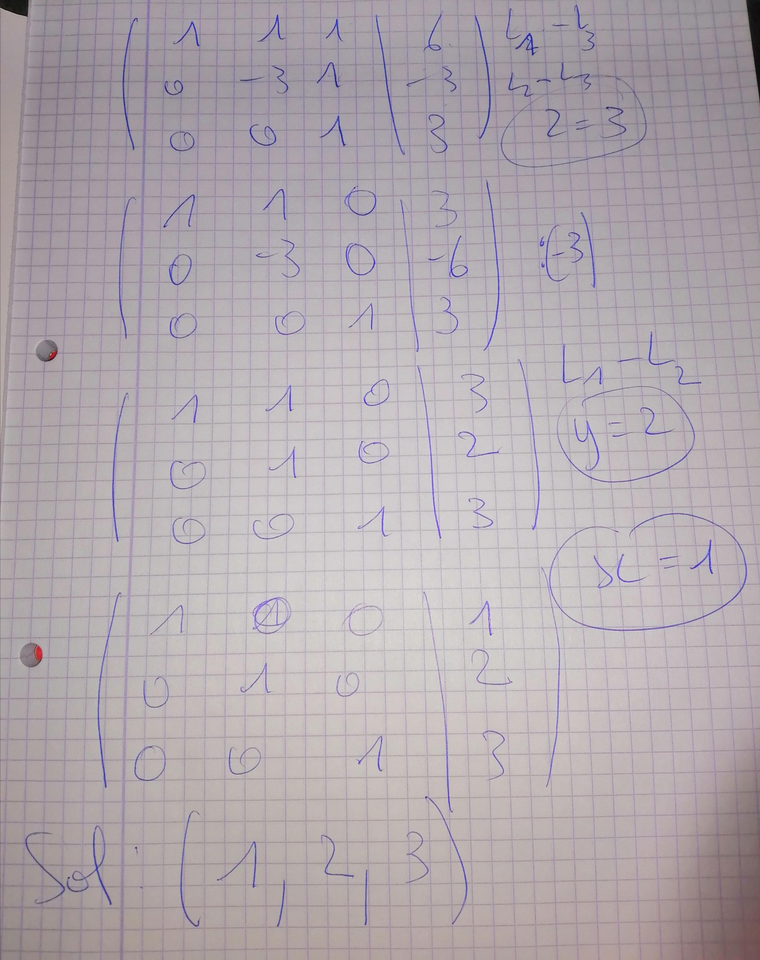
@Noemi Je pense avoir trouver la réponse , Est-ce correct svp ?
-
C'est correct.