suite arithmétique et géométrique
-
Joyca Le Boss dernière édition par
@Noemi
Bonsoir, j'ai un petit problème en maths sur les suites arithmétique et géométrique
voici l'énoncé.
Apprenti jardinier, Isaac travaille dans un joli jardin d’une surface de 1500 m² de
gazon. Chaque année, 20 % est utilisée pour un potager durant l’été. Tous les ans
en octobre, Isaac enlève 70 m² du potager et le remplace par du gazon.
Les aires sont exprimées en m², arrondies à l’unité.-
L’aire initiale 𝑢0 = 1500 et on note
𝑢𝑛 𝑙𝑎 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝑑𝑒 𝑔𝑎𝑧𝑜𝑛 𝑠𝑎𝑛𝑠 𝑝𝑜𝑡𝑎𝑔𝑒𝑟 restant au bout de 𝑛 autonmes.
Justifier que pour tout entier naturel n, on a 𝑢𝑛+1 = 0.8𝑢𝑛 + 70 -
Calculer l’aire de la pelouse à la fin de l’automne de la première année, puis la
fin de l’automne de la deuxième année. (𝑢1 = ⋯
𝑒𝑡 𝑢2 = ) -
On considère la suite (𝒗𝒏) définie par 𝒗𝒏 = 𝒖𝒏 − 𝟐𝟕𝟎
a) Déterminer 𝒗𝒏+𝟏 en fonction de 𝒗𝒏
b) En déduire 𝒗𝒏 en fonction de n. -
Démontrer alors que, pour tout entier naturel n, on a 𝒖𝒏 = 𝟏𝟐𝟑𝟎 ∗ 𝟎. 𝟖
𝒏 + 𝟐𝟕𝟎 -
Calculer l’aire de la pelouse (gazon sans le potager) au bout de 10 automnes.
-
Déterminer le sens de variation de la suite (𝒖𝒏).
-
Isaac se demande après combien d’années l’aire de la pelouse sera inférieure à 200 m² ?
-
-
@Joyca-Le-Boss Bonsoir,
Indique tes calculs et la question qui te pose problème.
-
Joyca Le Boss dernière édition par
@Noemi
L’aire initiale 𝑢0 = 1500 et on note
𝑢𝑛 𝑙𝑎 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝑑𝑒 𝑔𝑎𝑧𝑜𝑛 𝑠𝑎𝑛𝑠 𝑝𝑜𝑡𝑎𝑔𝑒𝑟 restant au bout de 𝑛 autonmes.
Justifier que pour tout entier naturel n, on a 𝑢𝑛+1 = 0.8𝑢𝑛 + 70Cela me pose problème, je suis bloqué à partir de là
-
Joyca Le Boss dernière édition par
@Noemi
je n'arrive pas à trouvé la raison.
Pouvez vous me dire quelle formule utilisé ?
-
Chaque année 20% est utilisé pour le potager, donc il reste 1-20% = ...
et ensuite on ajoute 70 m2m^2m2 de gazon.
donc un+1=....u_{n+1}= ....un+1=....
-
Joyca Le Boss dernière édition par
Ce message a été supprimé !
-
Joyca Le Boss dernière édition par
donc si j'ai bien compris je doit soustraire 1 (qui est l'année)par 20%
et ensuite je doit multiplié 70m² par le résultat trouvée
est ce correct ?
-
Joyca Le Boss dernière édition par
@Noemi
il y a une chose que je n'ai pas compris vous avez soustrait 1 par 20% mais le 1 n'a aucune unité au finale le résultat donnera
moins19% ou moins19 tout court ?
-
-
Joyca Le Boss dernière édition par
@Noemi
donc un+1=?
-
L'énoncé te donne la réponse :
un+1=0,8un+70u_{n+1}=0,8u_n+70un+1=0,8un+70Passe à la question 2, sachant que u0=1500u_0=1500u0=1500.
-
Joyca Le Boss dernière édition par
@Noemi
OK, devons nous pas trouvé Un?
-
Non
La question 2 demande de calculer u1u_1u1 et u2u_2u2.
Donc comme
un+1=0,8un+70u_{n+1}=0,8u_n+70un+1=0,8un+70
Et sachant que u0=1500u_0=1500u0=1500.
Tu remplaces nnn par 0, soit
u1=0,8u0+70=0,8×1500+70=...u_1=0,8u_0 + 70 = 0,8\times 1500 +70 = ...u1=0,8u0+70=0,8×1500+70=...Puis tu remplaces nnn par 1.
....
-
Joyca Le Boss dernière édition par
@Noemi
J'ai trouvé 1270 pour U1
et pour U2 j'ai trouvée 1200
Est-ce correct ?
-
u1u_1u1 est juste
u2u_2u2 est faux;
u2=0,8×u1+70u_2=0,8\times u_1+70u2=0,8×u1+70
-
Joyca Le Boss dernière édition par
@Noemi
donc U2=1086 ?
Et la question 3 je suis perdu je sais pas comment procéder.
Dois-je utilisé la même formule que la deuxième question ?
-
u2u_2u2 est juste.
Question 3 :
vn+1=un+1−270v_{n+1}=u_{n+1}-270vn+1=un+1−270
Remplace un+1u_{n+1}un+1 par son expression en fonction de unu_nun.
Puis simplifie l'expression.
-
Joyca Le Boss dernière édition par
@Noemi
donc je remplace Un+1 par 0,8Un+70
vue que Un+1=0,8Un=70
c'est à dire que 0,8Un=70 et l'expression de Un+1 ?
je me trompe ou pas ?
-
Tu te trompes.
Tu dois écrire vn+1v_{n+1}vn+1 en fonction de unu_nun puis de vnv_nvn.
-
Joyca Le Boss dernière édition par
@Noemi
vous pouvez me donnez un indice ?
-
Joyca Le Boss dernière édition par
@Joyca-Le-Boss
SVP
-
J'ai indiqué ce qu'il fallait faire :
vn+1=un+1−270v_{n+1}=u_{n+1}-270vn+1=un+1−270
Remplace un+1u_{n+1}un+1 par son expression en fonction de unu_nun.
Soit remplacer un+1u_{n+1}un+1 par 0,8un+700,8u_n+700,8un+70.
Puis simplifie l'expression.L'expression de vnv_nvn est-elle correcte ?
-
Joyca Le Boss dernière édition par
@Noemi
Oui, elle est correct
-
Joyca Le Boss dernière édition par
@Noemi
Non, elle n'est pas correct pardon ce n'est pas Vn+1=UIn+1−270 c'est Vn=Un-270
il n'y a pas de n+1 dans le troisième exercices
-
Indique tes calculs pour la question 3.
-
Joyca Le Boss dernière édition par
@Noemi
donc j'ai fait une égalité Vn=Vn+1
en sachant que Vn=Un-270 mais a partir de la je bloque car je ne vois pas à quoi correspond Vn+1
-
Joyca Le Boss dernière édition par
@Noemi
est ce le bon procéder pour Déterminer 𝒗𝒏+𝟏 en fonction de 𝒗𝒏 ?
-
Ecrire sans le démontrer que vn+1=vnv_{n+1}=v_nvn+1=vn est faux.
Reprend mes indications ou je te demande juste de remplacer (écrire à la place).
-
Joyca Le Boss dernière édition par
@Noemi
vous vous êtes trompé dans la consigne je pense car sur ma feuille il y a écrit Vn=Un-270 ET pas Vn+1=Un+1-270
-
Joyca Le Boss dernière édition par
@Noemi
Et si je remplace comme vous avez dit sa va me donner
Vn+1=0,8Un+70-270
est ce correct ?
-
Joyca Le Boss dernière édition par
@Noemi
Vous avez trouvé quoi pour l'ex 3a ?
-
Simplifie l'expression, tu trouves
vn+1=0,8un−200v_{n+1}=0,8u_n-200vn+1=0,8un−200
puis tu remplaces
unu_nun par vn+270v_n+270vn+270
soit
vn+1=0,8(vn+270)−200v_{n+1}=0,8(v_n+270) - 200vn+1=0,8(vn+270)−200
= ....vérifie l'énoncé.
-
Joyca Le Boss dernière édition par
@Noemi Exscusez moi donc la reponse pour la premier question c'est juste :
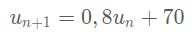
Donc c'est une Suite Arithmetique !
La dans la question 1 on nous U0 = 1500 ! et on nous indique egalement que n egale a tout entier naturel mais la vrai question est Comment justifier que tout entier naturel n , on a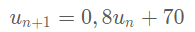
Pouvez-vous m'aider à le justifier svp ?
-
Ce n'est pas une suite arithmétique, il faudrait que ce soit de la forme :
un+1=un+ru_{n+1}=u_n+run+1=un+r
J'ai indiqué les éléments de réponse pour la première question.Vérifie l'énoncé !!
-
Joyca Le Boss dernière édition par
@Noemi Pouvez-vous me les résumés pour que ca soit plus correct svp ?
-
Reprends mes réponses.
-
Joyca Le Boss dernière édition par
@Noemi donc pour la question 1 ,il faut le justifier en notant juste ca
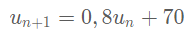
Est-ce correct ?
-
Non,
Regarde mes réponses.
Chaque année 20% est utilisé pour le potager, donc il reste 1-20% = ...
et ensuite on ajoute 70 m2m^2m2 de gazon.
donc un+1=....u_{n+1}= ....un+1=....
-
Joyca Le Boss dernière édition par
Ce message a été supprimé !
-
Joyca Le Boss dernière édition par
@Noemi
donc la réponse à la 1er question c'est 0,8+70=Un+1
Est ce correct?
et doit on rajouté quelque chose d'autre ou on s'arrête là ?
-
@Joyca-Le-Boss
NonCompléte :
Chaque année 20% est utilisé pour le potager, donc il reste 1-20% = ...
et ensuite on ajoute 70 m270 \ m^270 m2 de gazon.
donc un+1=....u_{n+1}=....un+1=....
-
Joyca Le Boss dernière édition par
@Noemi
Donc la réponse vu que vous m'avez dit d'additionner .
Un+1 =0,8+70m²
Est-ce correct?
-
Il manque unu_nun.
-
Joyca Le Boss dernière édition par
@Noemi
La réponse du première exercice est
Un+1=0,8Un+70m²
Je me trompe ?
-
C'est la réponse, mets l'unité à part.
-
Joyca Le Boss dernière édition par
@Noemi
Je dois 'isoler ?
comment dois je faire?
-
Joyca Le Boss dernière édition par
@Noemi
je pense que j'ai trouvé les réponses à la question 3A :On considère la suite (𝒗𝒏) définie par 𝒗𝒏 = 𝒖𝒏 − 𝟐𝟕𝟎
a) Déterminer 𝒗𝒏+𝟏 en fonction de 𝒗𝒏
b) En déduire 𝒗𝒏 en fonction de n.
donc pour déterminer Vn+1 en fonction de Vn j'ai fais;
𝒗𝒏+𝟏=0,8un+70
𝒗𝒏+𝟏=0,8Un+70-270
𝒗𝒏+𝟏=0,8Un-200
𝒗𝒏+𝟏=0,8(Vn+270)-200
𝒗𝒏+𝟏=0,8Vn+216-200
𝒗𝒏+𝟏=Vn+16
Est-ce correrct?
et la question b j'ai rien trouver pourriez vous me montrer vos réponse pour la question b ?
-
Une erreur à la fin.
Tu dois trouver
vn+1=0,8vn+16v_{n+1}=0,8v_n+16vn+1=0,8vn+16La suite n'est pas géométrique donc à mon avis il y a une erreur dans l'énoncé, d'ou ma demande de vérifier l'énoncé.
-
Joyca Le Boss dernière édition par
@Noemi
l'énonce de l'exercice 3 ou 1 ?
-
L'énoncé de cet exercice.
-
Joyca Le Boss dernière édition par
@Noemi
voici la consigne de l'exercice 3
On considère la suite (𝒗𝒏) définie par 𝒗𝒏 = 𝒖𝒏 − 𝟐𝟕𝟎
a) Déterminer 𝒗𝒏+𝟏 en fonction de 𝒗𝒏
b) En déduire 𝒗𝒏 en fonction de n
-
Joyca Le Boss dernière édition par
@Noemi
vous pouvez me montrer vos calcule pour voir ou est mon erreur ?
-
Tu as écris :
vn+1=0,8vn+216−200v_{n+1}=0,8v_n+216-200vn+1=0,8vn+216−200
puis : vn+1=vn+16v_{n+1}=v_n+16vn+1=vn+16 0u est passé le 0,8 ???Donc vn+1=0,8vn+16v_{n+1}=0,8v_n+16vn+1=0,8vn+16
-
Joyca Le Boss dernière édition par
@Noemi
ah oui désoler c'est une erreur de frapper.
Et le raisonnement est il juste est ce la meilleur manière de déterminer 𝒗𝒏+𝟏 en fonction de 𝒗𝒏 ?
-
Oui le calcul est juste.
-
Joyca Le Boss dernière édition par
@Noemi
ok merci , mais j'ai un petit problème pour l'exercice 3 b je ne sais pas comme procédé voici la consigne :
On considère la suite (𝒗𝒏) définie par 𝒗𝒏 = 𝒖𝒏 − 𝟐𝟕𝟎b) En déduire 𝒗𝒏 en fonction de n
je suis bloquer ?
pouvez vous me montrer vos calcul ?
-
Pour la question 3 b), tu dois utiliser le résultat de la question 3 a)
Vu que tu n'obtiens pas une suite géométrique, il faut faire une transformation.
Soit définir une nouvelle suite :
wn=vn−80w_n= v_n-80wn=vn−80 et procéder comme pour la question 3 a.
-
Joyca Le Boss dernière édition par
@Noemi
donc
Wn=Vn −80
Wn=(0,8+16)-16=>car Vn+1=0,8+16
Wn=0,8+16-16=0,8
Wn=0,8
est ce correct?
-
Non, tu as oublié vnv_nvn.
-
Joyca Le Boss dernière édition par
@Noemi
je ne vois pas mon erreur. Pourriez vous détailler d'avantage SVP ?
-
Reprends les calculs depuis le début
wn+1=vn+1−80w_{n+1}=v_{n+1}-80wn+1=vn+1−80
wn+1=0,8vn+16−80w_{n+1}=0,8v_{n}+16-80wn+1=0,8vn+16−80
....
-
Joyca Le Boss dernière édition par
@Noemi
lorsque je vais faire le calcule en simplifiant par quoi devrais je remplacer Vn ?
-
Tu remplaces vnv_nvn par wn+80w_n+80wn+80.
-
Joyca Le Boss dernière édition par
@Noemi
donc j'ai fais
Wn+1=Vn+1-80
Wn+1=0,8+16-80
Wn+1=0,8×(Wn+80)+16-80
Wn+1=0,8Wn+64-64
Wn+1=0,8Wn
Est ce correct ?
-
Il manque vnv_nvn à la deuxième ligne.
Le résultat est correct, tu en déduis la nature de la suite wnw_nwn puis tu peux exprimer wnw_nwn en fonction de nnn.
-
Joyca Le Boss dernière édition par
@Noemi
vous pouvez me donner la déduction de la nature de la suite ?
-
C'est du cours.
C'est une suite géométrique de premier terme w0w_0w0 à calculer et de raison 0,8.
-
Joyca Le Boss dernière édition par
Ce message a été supprimé !
-
Joyca Le Boss dernière édition par
@Noemi
donc la nature de la suite est géométrique !
et comment peut on exprimer Wn en fonction de N ?
-
C'est du cours.
-
Joyca Le Boss dernière édition par
@Noemi
Voici se que j'ai trouvé pour la question suivant :
4: Démontrer alors que, pour tout entier naturel n, on a 𝒖𝒏 = 𝟏𝟐𝟑𝟎×𝟎. 𝟖𝒏 + 𝟐𝟕𝟎
Comme Vn=Un-270 =>Un=Vn+270
donc Un=1230× 0,8n+270
-
Joyca Le Boss dernière édition par
@Noemi
est ce correct ?
-
Non,
Il faut démontrer en utilisant les résultats de la question 3 b).
Question que tu dois terminer.De plus il n'est pas possible d'arriver à ce résultat, d'ou mes multiples remarques pour que tu vérifies l'énoncé. Demande à ton professeur ou à tes camarades pour vérifier l'énoncé.
-
Joyca Le Boss dernière édition par
@Noemi
l'énoncé de la question 3 B OU A ?
-
Joyca Le Boss dernière édition par
@Noemi Vous pouvez m'indiquer précisément ce qui cloche dans l'énoncé ?
-
-
Joyca Le Boss dernière édition par
@Noemi
Mais le problème c'est que j'arrive pas à le terminé !
-
Joyca Le Boss dernière édition par
@Noemi
Vous pouvez me donner la réponse parce que je suis bloqué SVP ?
-
Tu devrais regarder le cours
suite géométrique : un=u0×qnu_n= u_0\times q^nun=u0×qn
-
Joyca Le Boss dernière édition par
@Noemi
merci
donc je remplace U0 par quoi ?
-
u0u_0u0 correspond à la valeur du premier terme de la suite.
-
Joyca Le Boss dernière édition par
@Noemi
donc sa ne peux pas être 0,8 car c'est la raison de la suite
donc le premiers terme de la suite est 1500 ?
Est ce correct ?
-
Pour la suite unu_nun c'est bien u0=1500u_0=1500u0=1500
calcule le premier terme de la suite vnv_nvn puis de la suite wnw_nwn.
-
Joyca Le Boss dernière édition par
@Noemi
Donc le premier terme de la suite vn
c'est V1=1500×q exposant 1
Est-ce correct ?
-
-
Joyca Le Boss dernière édition par
@Noemi
Je suis perdu .Pouvez vous m'éclaircir en me disant de quelle relation vous parler ?
-
vn=un−270v_n= u_n-270vn=un−270
-
Joyca Le Boss dernière édition par
@Noemi
Je ne sais pas comment procéder
-
Joyca Le Boss dernière édition par
@Noemi
je pense que c'est
Vn=1500.qexposant n -270
Est ce correct ?
-
vn=un−270v_n= u_n-270vn=un−270
si n=0n=0n=0, v0=u0−270v_0= u_0-270v0=u0−270de même
wn=vn−80w_n= v_n-80wn=vn−80
w0=v0−80w_0= v_0-80w0=v0−80
-
Joyca Le Boss dernière édition par
@Noemi
Je continue simplifier ?
Ou c'est la réponse?
-
Joyca Le Boss dernière édition par
@Noemi
donc si je remplace U0 par 1500 cela me donnera
Vo=1500-270=1230
donc vo=1230
et même chose pour l'autre
Wo=1230-80= 1150 Est ce correct ?
-
C'est correct.
Tu peux donc écrire maintenant la relation de
wnw_nwn en fonction de nnn.
-
Joyca Le Boss dernière édition par
@Noemi
je doit encore rajoute quelque chose ?
-
Joyca Le Boss dernière édition par
@Noemi
peut on répondre à la 4 EM question ?
-
La relation de wnw_nwn en fonction de nnn.
puis de vnv_nvn en fonction de nnn.
puis pour la question 4 de unu_nun en fonction de nnn.
-
Joyca Le Boss dernière édition par
@Noemi
Pouvez vous me donnez un indice pour que je fasse la relation SVP ?
-
J'ai déjà donné la relation, visiblement tu fais peu d'effort. Tu attends que je réalise l'exercice a ta place ce que je ne souhaite pas faire .
wn=1150×0,8nw_n=1150 \times 0,8^nwn=1150×0,8n
vn=1150×0,8n+80v_n=1150 \times 0,8^n+80vn=1150×0,8n+80
Question 4) on déduit
un=1150×0,8n+80+270=....u_n=1150 \times 0,8^n+80+270 = ....un=1150×0,8n+80+270=....Ce qui n'est pas égal à la relation indiquée dans l'énoncé d'ou il doit y avoir une erreur.
-
mtschoon dernière édition par mtschoon

Bonjour,
Seulement une remarque.
Comme le dit @Noemi , il y a une erreur dans cet énoncé car (Vn)(V_n)(Vn) doit être géométrique . C'est un classique !
Une chose surprenante : avec des données différentes et le même texte, il y a un exercice similaire ici, et sans erreur...
c'est l'exercice 2
https://www.annales2maths.com/1s-exercices-suites/
Bizarre...
-
Joyca Le Boss dernière édition par
@mtschoon
ok, je vais essaye de voir d'où viens le problème avec mon prof
et merci à vous et à @Noemi
-
Joyca Le Boss dernière édition par
-
Soit il se trompe, soit c'est l'énoncé qui comporte une erreur.
-
mtschoon dernière édition par mtschoon

C'est sûr qu'il y a une erreur dans l'énoncé écrit ...
Si les autres données sont bonnes ( ce que j'ignore ! ), pour que la suite (Vn)(V_n)(Vn) soit géométrique, il faudrait :
Vn=Un−350\boxed {V_n=U_n-350}Vn=Un−350 et non Vn=Un−270V_n=U_n-270Vn=Un−270CALCUL :
Vn+1=Un+1−350V_{n+1}=U_{n+1}-350Vn+1=Un+1−350
Vn+1=0.8Un+70−350V_{n+1}=0.8U_n+70-350Vn+1=0.8Un+70−350
Vn+1=0.8(Vn+350)+70−350V_{n+1}=0.8(V_n+350)+70-350Vn+1=0.8(Vn+350)+70−350
Vn+1=0.8Vn+(0.8×350)+70−350V_{n+1}=0.8V_n+(0.8\times 350)+70-350Vn+1=0.8Vn+(0.8×350)+70−350
Vn+1=0.8Vn+280+70−350V_{n+1}=0.8V_n+280+70-350Vn+1=0.8Vn+280+70−350
Vn+1=0.8Vn+350−350V_{n+1}=0.8V_n+350-350Vn+1=0.8Vn+350−350
Vn+1=0.8VnV_{n+1}=0.8V_nVn+1=0.8Vn
Suite géométrique.@Joyca-Le-Boss , je te conseille de contacter à nouveau ton professeur (si tu es sûr que l'énoncé que tu as écrit est bien celui donné par ton professeur).
-
mtschoon dernière édition par mtschoon

Bonjour,
Quelques pistes pour la fin de cet exercice avec la modification proposée pour la suite auxiliaire (Vn)(V_n)(Vn)
Vn+1=0.8VnV_{n+1}=0.8V_nVn+1=0.8Vn
V0=U0−350=1500−350=1150V_0=U_0-350=1500-350=1150V0=U0−350=1500−350=1150
(Vn)(Vn)(Vn) suite géométrique de raison q=0.8q= 0.8q=0.8 et de premier terme V0V_0V0
Donc :Vn=V0qn=1150(0.8)nV_n=V_0q^n=1150(0.8)^nVn=V0qn=1150(0.8)nUn=Vn+350=1150(0.8)n+350U_n=V_n+350=\boxed{1150(0.8)^n+350}Un=Vn+350=1150(0.8)n+350
Pour n=10n=10n=10, V10≈473.48 (m2)V_{10}\approx 473.48\ \ (m^2)V10≈473.48 (m2)
0<0.8<10\lt 0.8\lt 10<0.8<1 donc :
(Un)(U_n)(Un) strictement décroissante
limn→+∞0.8n=0\displaystyle {\lim_{n\to +\infty} 0.8^n=0}n→+∞lim0.8n=0
limn→+∞Un=350\displaystyle {\lim_{n\to +\infty} U_n=350}n→+∞limUn=350
Il n'est pas possible que l'aire de la pelouse soit inférieure à 200 m2m^2m2
-
mtschoon dernière édition par mtschoon

Quelques illustrations avec un tableau,
Valeurs (approchées ) de UnU_nUn pour les premières valeurs de n
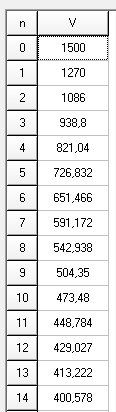
Valeurs (approchées) pour de plus grandes valeurs de n.
(pour n≥66n\ge 66n≥66, les valeurs de UnU_nUn sont tellement proches de 350350350, que le tableur arrondit à 350350350)
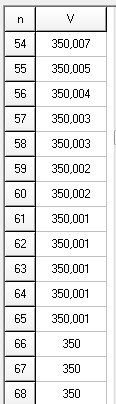
Bonne lecture.