exercice sur le logarithme népérien
-
Rania Belaidouni dernière édition par
Bonjour, j'ai un peu de mal, avec 3 exercices, pouvez-vous m'aider. Les voici:
Exercice 1
La fonction f est définie sur l'intervalle ]0;+00[ par f(x)=4x-xln(x).
Mila à obtenu à l'aide de sa calculatrice une partie de la courbe représentative de la fonction f présenté ci-contre (On voit une courbe croissante).
Elle émet la conjecture suivante:
"Il semble que la fonction f est positive"a) Résoudre dans ]0;+00[ l'équation f(x)=0
Donc voila ce que j'ai fait, je pense que c'est juste, mais on sait jamais:4x-xln(x)=0
x(4-ln(x))=0
Donc x=04-ln(x)=0
-ln(x)=-4
ln(x)=4
x=e^4b) Déterminer le signe de f(x) sur ]0;+00[
limite quand x tend vers 0 de 4x-xln(x)=?
limite quand x tend vers 0 de 4x=0
Limite quand x tend vers 0 de -xln(x)=0
Donc par somme la limite de f(x) quand x tend vers 0=0Limite quand x tend vers +00 de f(x)=?
x(4-(xln(x)/x)=+00c)Expliquer pourquoi Mila à pue penser que sa conjecture était vraie.
Je ne comprend pas vraiment, j'ai dû faire une erreur précédemment.Voila, j'ai un peu de mal. Merci d'avance.
-
@Rania-Belaidouni Bonjour,
Pour déterminer le signe de la fonction, il faut étudier ses variations.
Calcule la dérivée et étudie son signe.
-
BBlack-Jack dernière édition par
Bonjour,
Attention, la solution x = 0 (pour la question a) est fausse.
Je te laisse trouver pourquoi.
-
Rania Belaidouni dernière édition par
D'accord merci, je vais continuer, si j'ai besoin d'aide je vous ferez signe.
-
Rania Belaidouni dernière édition par
@Noemi a dit dans exercice sur le logarithme népérien :
Calcule la dérivée et étudie son signe.
Donc j'ai calculé la dérivée:
f(x)=4x-xln(x)
f'(x)=4-1x(1/x)f'(x)=4x-1(1/x)=0
Donc x est différent de 0
-1/x=-4
1=4x
4x=1
x=1/4On peut faire le tableau de signe
Avec entre 0 et 1/4 c'est -
et entre 1/4 et +00 c'est +
Donc f est décroissant entre 0 et 1/4 et croissant sur 1/4 et +00Ensuite pour ça je ne suis pas sur :
La limite quand x tend vers 0 est = +00
La limite quand x tend vers +00 est de +00
-
Attention, la dérivée est
f′(x)=4−ln(x)−x×1x=....f'(x)= 4-ln(x)-x\times \dfrac{1}{x} = ....f′(x)=4−ln(x)−x×x1=....
-
Rania Belaidouni dernière édition par
3-ln(x)-1 c'est bien cela ?
-
Non : f′(x)=3−ln(x)f'(x) = 3-ln(x)f′(x)=3−ln(x)
Résous f′(x)=0f'(x) = 0f′(x)=0 et cherche le signe de la dérivée.
-
Rania Belaidouni dernière édition par
Ca me donne x=e^3
Donc on peut faire le tableau tableau de signe
entre 0 et e^3 le signe de f'(x) est +
donc f est croissant. C'est le contraire entre e^3 et +00.Ensuite pour les limites:
limite quand x tend vers 0 =-00
limite quand x tend vers +00=+00Voila c'est bien cela? Et pour la conjecture de Mila, elle à du faire la même erreur que moi, c'est à dire calculé la limite à partir de f(x) et non de f'(x).
-
Pour les variations de la fonction, il faut calculer les limites de la fonction et non de la fonction dérivée.
As-tu tracé la fonction sur la calculatrice ?
-
Rania Belaidouni dernière édition par
Oui d'accord donc cela nous fait :
lim quand x tend vers 0 de 4x-xln(x)=0
lim 4x=0
lim-xln(x)=0
Donc par somme =0lim quand x tend vers +00 de f(x)=
c'est surement égal à -00 mais je n'arrive pas à le prouver
Donc par somme = -00
-
Pour la limite en +∞+\infty+∞, mets xxx en facteur.
Le résultat est bien −∞-\infty−∞.Puis tu conclus.
-
Rania Belaidouni dernière édition par
D'accord je ne savais pas et oui c'est ça.
-
J'ai transféré le sujet, répond sur le nouveau sujet.
As-tu fait la conclusion pour la question 1 de cet exercice ?
-
mtschoon dernière édition par mtschoon

Bonjour,
Une représentation graphique pour éclairer (peut-être) cet exercice.
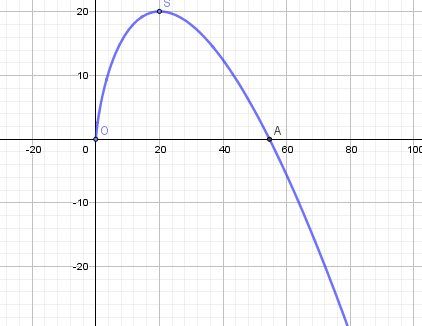
La fonction f est définie sur ]0,+∞[]0,+\infty[]0,+∞[, car la condition d'existence est x>0x\gt 0x>0, à cause du logarithme.
La représentation graphique est la courbe en bleu, le point O(0,0) est non compris vu que x>0x\gt 0x>0
limx→0+f(x)=0\displaystyle \lim_{x\to 0^+}f(x)=0x→0+limf(x)=0
limx→+∞f(x)=−∞\displaystyle \lim_{x\to +\infty}f(x)=-\inftyx→+∞limf(x)=−∞
Le sommet S de la courbe a pour coordonnées (e3;e3)(e^3;e^3)(e3;e3)
Le pont d'intersection de la courbe avec l'axe des abscisses est l'unique point A de coordonnées (e4,0)e^4,0)e4,0)Conclusion :
La partie de courbe que voit Mila ( schéma que tu ne donnes pas ) doit être une portion de la partie d'abscisse x∈]0,e3]x\in ]0,e^3]x∈]0,e3] vu que tu indiques que le fonction est croissante.
Bien sûr que sa conjecture est fausse vu que la fonction est strictement négative pour x∈]e4,+∞[x\in ]e^4,+\infty[x∈]e4,+∞[
-
Rania Belaidouni dernière édition par
De même que pour l'autre exercice, j'ai tous compris merci beaucoup.
-
C'est parfait si tu as tout compris.
-
mtschoon dernière édition par

Bravo !