Centre d'inertie d'une plaque homogène
-
Djenab Bangoura dernière édition par
Bonsoir svp je n'arrive pas à comprendre l'exo et je dois le rendre demain matin. Svp expliquer moi comment faire 🥺🥺🥺🥺🥺🥺🥺🥺🥺🥺.
Une plaque homogène est d'épaisseur constante ABCD a une forme trapézoïdale avec AB=BC=CD=a et la base AD=2a. Déterminer la position du centre d'inertie de cette plaque
-
@Djenab-Bangoura Bonsoir,
Décompose le trapèze en trois triangles équilatéraux.
Détermine le centre d'inertie de chaque triangle, au 2/3 de la hauteur.
Puis tu cherches le centre d'inertie du triangle formé par les trois centres d'inerties.Le centre d'inertie est sur l'axe de symétrie du trapèze, tu peux choisir un repère ayant pour abscisse la base du trapèze et ordonnée le centre de symétrie.
-
mtschoon dernière édition par mtschoon

Bonjour,
Je me permets un schéma dans le cas où la "forme trapézoïdale" serait un trapèze rectangle.
Vu l'énoncé écrit, ce n'est pas sûr, mais c'est plausible...
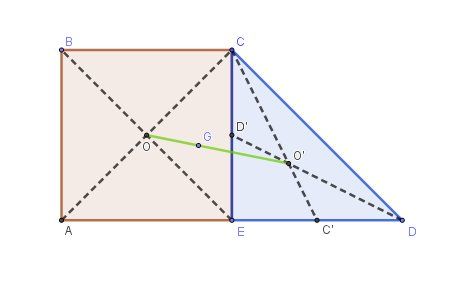
Dans ce cas simple,
le barycentre de (A,B,C,D) (centre d'inertie de la partie rectangulaire rose) est O (intersection des diagonales)
le barycentre de (E,D,C) ) (centre d'inertie de la partie triangulaire bleue ) est O' (intersection des médianes)Le point G cherché est le barycentre de O et O' affectés des coefficients proportionnels à leurs aires.
G=bar((O,2),(O′,1))G=bar((O,2),(O',1))G=bar((O,2),(O′,1))
GO→=−12GO′→\overrightarrow{GO}=-\dfrac{1}{2}\overrightarrow{GO'}GO=−21GO′(Je ne détaille pas plus, vu qu'il n'est pas sûr que ce soit ce cas qu'il fallait étudier, mais je l'imagine...)