les vecteurs mathématiques

Bonsoir
ABCD est un rectangle , les points E et H sont tels que AE=3/2AD et CH=2/3CD

a. décomposer le vecteur BE en passant par A puis exprimer BE sous la forme xAB+yAD

b. décomposer le vecteur HB en passant par C et exprimer HB sous la forme x'AB+y'AD
pouvez vous m'aidez svp

Indique tes éléments de réponse et la question qui te pose problème.

a. En utilisant la relation de Chasles :
$BE→=BA→+AE→\overrightarrow{BE}= \overrightarrow{BA}+\overrightarrow{AE}$
.....

@Noemi le question 1 me pose problème :
BE = BA + AE
BE = 3/2 AD + BA
est ce juste pour l'instant ?

@Livindiam-Livin

C'est correct, tu peux poursuivre.

Bonjour,

@Livindiam-Livin , vu la question posée, tu transformes encore.

$BE→=(−1)AB→+32AD→\overrightarrow{BE}=(-1) \overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}$

Pour pouvoir vérifier ta réponse, je t'indique ce que tu dois trouver pour $HB→\overrightarrow{HB}$

$HB→=23AB→+(−1)AD→\overrightarrow{HB}=\dfrac{2}{3}\overrightarrow{AB}+(-1)\overrightarrow{AD}$

Reposte si tu n'y arrives pas.

Un schéma pour illustration.

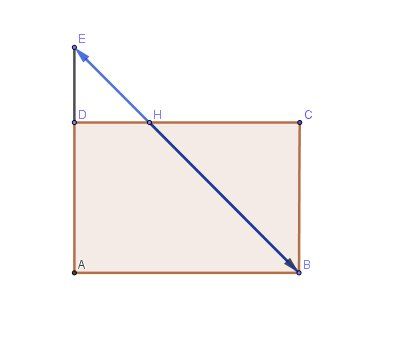
J'imagine que l'énoncé demande, après les questions indiquées, de justifier que les vecteurs étudiés sont colinéaires, puis que points B,H,E sont alignés.

@mtschoon bonjour
J'ai pris la correction mais je ne comprends pas le principe , est ce que vous pourriez m'expliquer comment résoudre ce genre d'exercices svp ?

@Livindiam-Livin , bonjour,

Essaie de préciser ta question et ce qui te pose problème.

@mtschoon bonsoir
la question qui me posent problèmes sont comment exprimer HB sous la forme de x'AB + y'AD je ne comprends pas

@Livindiam-Livin

L'énoncé te précise ce qu'il faut faire.

En passant par le point C :
$HB→=HC→+CB→\overrightarrow{HB}= \overrightarrow{HC}+\overrightarrow{CB}$
...

@Livindiam-Livin ,

J'essaie de détailler le mieux possible.

Comme vient de te le dire Noemi, et d'après ce que l'indique l'énoncé , avec la relation de Chasles :

$HB→=HC→+CB→\overrightarrow{HB}=\overrightarrow{HC}+\overrightarrow{CB}$

Tu transformes ensuite chacun de ces deux vecteurs.

a) L'énoncé t'indique que : $CH→=23CD→\overrightarrow{CH}=\dfrac{2}{3}\overrightarrow{CD}$
Tu prends l'opposé (regarde les propriétés de ton cours)
$HC→=23DC→\overrightarrow{HC}=\dfrac{2}{3}\overrightarrow{DC}$

Vu que le quadrilatère est un rectangle, $DC→=AB→\overrightarrow{DC}=\overrightarrow{AB}$

Donc $HC→=23AB→\boxed{\overrightarrow{HC}=\dfrac{2}{3}\overrightarrow{AB}}$

b)Vu que le quadrilatère est un rectangle,
$CB→=DA→\overrightarrow{CB}=\overrightarrow{DA}$
Donc
$CB→=−AD→\overrightarrow{CB}=-\overrightarrow{AD}$
c'est à dire
$CB→=(−1)AD→\boxed{\overrightarrow{CB}=(-1)\overrightarrow{AD}}$

c) En remplaçant les deux vecteurs $HC→\overrightarrow{HC}$ et $CB→\overrightarrow{CB}$ par les expressions trouvées, tu peux conclure que :
$HB→=23AB→+(−1)AD→\boxed{\overrightarrow{HB}=\dfrac{2}{3}\overrightarrow{AB}+(-1)\overrightarrow{AD}}$

CONCLUSION :
$x′=23\boxed{x'=\dfrac{2}{3}}$ et $y′=−1\boxed{y'=-1}$

Revois bien ton cours et regarde cela de près.

Bon travail.

@mtschoon je comprends mieux maintenant merci pour votre aide

@Livindiam-Livin , de rien.
Essaie de faire l'exercice sans regarder l'aide, pour être sûr(e) de bien maîtriser.

@mtschoon Bonjour
J'ai encore du mal avec cette exercice, je comprends qu'il faut changer AE en 3/2 AD mais pourquoi on ne change pas BA en -2/3 étant donné que sur la figure BA=CD et dans l'énoncé CH=2/3CD

@Livindiam-Livin , bonjour,

L'énoncé te demande d'exprimer les vecteurs en fonction de $AB→\overrightarrow{AB}$ et $AD→\overrightarrow{AD}$

Donc le vecteur $BA→\overrightarrow{BA}$ doit s'exprimer en fonction de $AB→\overrightarrow{AB}$ :

$BA→\overrightarrow{BA}$ est l'opposé de $AB→\overrightarrow{AB}$

$BA→=−AB→=(−1)AB→\overrightarrow{BA}=-\overrightarrow{AB}=(-1)\overrightarrow{AB}$

@mtschoon d'accord merci !

De rien @Livindiam-Livin ,

Bon travail.