Calcul d'inertance, de résistance et de compliance
-
?Un Ancien Utilisateur dernière édition par
Bonjour, j'aurais besoin de vérifications et d'aide sur un exercice d'application.
Sujet:
Le schéma ci-dessous est analogue à un cathéter hydraulique pour la mesure de la pression artérielle.
Pi représente la pression artérielle à l'entrée du cathéter et Po représente la pression exercée sur le diaphragme au bout du cathéter.
Bon à savoir: la catheter a une section de 5mm² et une longueur équivalente à 0.5m.
La solution saline dans le cathéter a une masse volumique de 1000 kg/m3 et une viscosité de 0.001 Pa s.
La chute de pression le long du cathéter est évaluée à 500 Pa pour un débit constant de 0.1 mL/s.
L’injection de 0.1 μL de liquide supplémentaire dans le cathéter cause un changement de la pression de 200Pa suite à la présence de bulles d'air et de 5 kPa sans bulles d'air.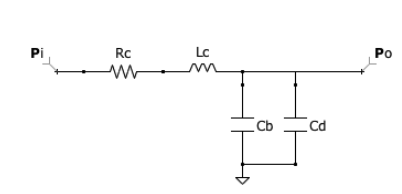
- DOnner l'inertance Lc du liquide et la résistance Rc du cathéter:
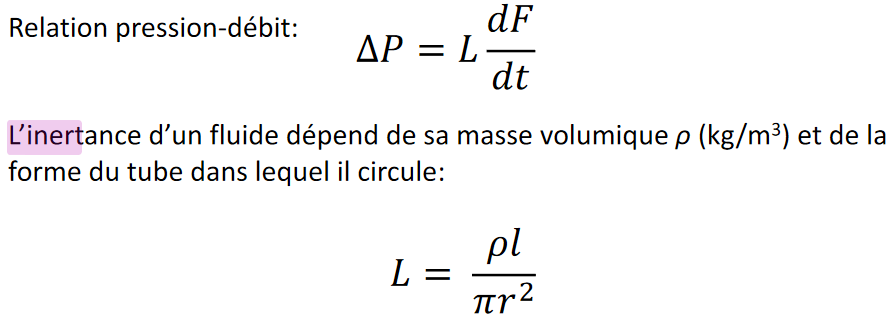
J'ai utilisé cette formule qui m'a donné 1000∗0,5PI∗(2.52∗10−3)2\frac{1000*0,5}{PI*(2.52*10^{-3})^2}PI∗(2.52∗10−3)21000∗0,5 = 25062191.84 Pa S²/m^3

Pour la résistance j'ai utilisé la formule ci-dessus.
8∗0.001∗0.5PI∗(2.52∗10−3)4\dfrac{8*0.001*0.5}{PI*(2.52*10^-3)^4}PI∗(2.52∗10−3)48∗0.001∗0.5 = 31572426.11 Pa S/m^3Je trouve les deux résultats obtenus très élevé.....
Question b) Trouver par le calcul la compliance du diaphragme Cd et la compliance aquivalente de l'ensemble des bulles d'air représenté par Cb.
J'ai envie d'utiliser:

mais je bloque un peu. est-ce la bonne voie?Excellent week-end
- DOnner l'inertance Lc du liquide et la résistance Rc du cathéter:
-
@anesthesiste Bonjour,
Pour les deux premiers calculs, revois le calcul du rayon.
L'énoncé indique la section : S=π×r2=5 mm2S=\pi\times r^2= 5 \ mm^2S=π×r2=5 mm2
-
?Un Ancien Utilisateur dernière édition par
Bonjour @Noemi
Je tente r= 2*(racine(5/PI))= 7.9266?
-
@anesthesiste
r2=Sπr^2=\dfrac{S}{\pi}r2=πS
soit r=Sπr=\sqrt{\dfrac{S}{\pi}}r=πS.
-
?Un Ancien Utilisateur dernière édition par
Bonjour Noemi,
merci.
J'obtiens grâce à la formule r=1.261566261Donc pour l'inertance LC=100 Pa S²/m^3
Pour RC = 5.03 *10^-4 Pa S/m^3
-
@anesthesiste
Tu as pris en compte les unités ?
la valeur de rrr indiquée est en mm.
-
?Un Ancien Utilisateur dernière édition par
Non effectivement.
Je trouve maintenant LC= 99 999.74 Pa S²/m^3
Rc= 502.65 Pa S/m^3
-
@anesthesiste
Vérifie les calculs et l'unité.
-
?Un Ancien Utilisateur dernière édition par
Le problème doit venir de mon calcul de r.
r= racine( 5.10^-3 / PI) = 0.03989422804?
-
@anesthesiste
Non, le rayon était correct : r=1,26156... mmr= 1,26156... \ mmr=1,26156... mm
et 5 mm25 \ mm^25 mm2 donne 5×10−6 m25\times 10^{-6}\ m^25×10−6 m2
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
Si le rayon est correct les valeurs de la formule sont:
LC=1000∗0.5PI∗(1.261566261)2\frac{1000*0.5}{PI*(1.261566261)^2}PI∗(1.261566261)21000∗0.5
-
@anesthesiste
Attention aux unités
Pour LCLCLC tu peux écrire : LC=1000×0,55×10−6=108LC=\dfrac{1000\times 0,5}{5\times 10^{-6}}=10^8LC=5×10−61000×0,5=108
-
?Un Ancien Utilisateur dernière édition par
Je viens de comprendre. Je n'avais pas fait le rapprochement que le dénominateur = S= 5 mm2
Je vais refaire les calculs
-
?Un Ancien Utilisateur dernière édition par
Bonjour @Noemi
Pour RC je trouve 8∗0.001∗0.5(5∗10−6)2\frac{8*0.001*0.5}{(5*10^{-6})^2}(5∗10−6)28∗0.001∗0.5= 16716^7167 Pa S/m^3Par contre j'ai un problème de compréhension car:PI*r² = s
s= 5mm²Dans les formules on utilise 5 qui est en mm², est-ce que c'est gênant?
Parce que on fait 5*10^-6 donc on passe de mm² à m² mais le ² me pose problème, non?
-
@anesthesiste
Pour le calcul de RC,il faut utiliser la valeur du rayon.
1 mm=10−3 m1 \ mm = 10^{-3}\ m1 mm=10−3 m
et
1 mm2=10−6 m21 \ mm^2 = 10^{-6}\ m^21 mm2=10−6 m2
-
?Un Ancien Utilisateur dernière édition par
Bonjour @Noemi ,
Il faut utiliser pour RC utiliser la valeur 1,26156?
-
@anesthesiste
Oui, r=1,26156... mmr= 1,26156... \ mmr=1,26156... mm mais utilise :
r=1,26156 10−3... mr= 1,26156\ 10^{-3}... \ mr=1,26156 10−3... m
-
?Un Ancien Utilisateur dernière édition par
@Noemi
Alors je trouve pour RC = 8∗0.001∗0.5PI∗(1.26156∗10−3)4\frac{8*0.001*0.5}{PI*(1.26156*10^{-3})^4}PI∗(1.26156∗10−3)48∗0.001∗0.5=502664803.2 Pa S/m^3Est ce que c'est le résultat attendu?
-
@anesthesiste
Oui, le résultat du calcul est juste.
-
?Un Ancien Utilisateur dernière édition par
merci @Noemi
-
?Un Ancien Utilisateur dernière édition par
Je voulais aussi vous demander pour la question B, si j'utilise les bonnes formules:
Question b) Trouver par le calcul la compliance du diaphragme Cd et la compliance aquivalente de l'ensemble des bulles d'air représenté par Cb.
J'ai envie d'utiliser:

mais je bloque un peu. est-ce la bonne voie?
-
?Un Ancien Utilisateur dernière édition par
Bonjour,
J'ai toujours du mal à savoir comment appliquer les formules de compliance données ci-dessus.
Il me semble qu'il me manque des données????Bonne journée
-
@anesthesiste
Tu as le volume de liquide supplémentaire : 0,1μL0,1\mu L0,1μL
et la différence de pression 200 Pa.
-
?Un Ancien Utilisateur dernière édition par
Bonjour, si je comprends bien:
Delta V= 0.1Micro L
Delta P= 200 Pa
-
@anesthesiste
Oui.
-
?Un Ancien Utilisateur dernière édition par
Mais alors pourquoi 0.1MicroL/200Pa = 1/E à quoi correspond ce E?
Et dans l'énoncé il faut calculer la compliance du diaphragme cd et la compliance équivalente de la totalité de bulles d'air Cb
Comment je fais la distinction entre les deux calculs?
-
@anesthesiste
Tu utilises la variation de pression avec ou sans bulles d'air.
-
?Un Ancien Utilisateur dernière édition par
Sans bulles d'air: 5*10^3/0,1 MicroL
Avec bulles: 200/0.1 MicroL
Par contre je ne suis pas sûr pour DeltaV= 0.1 MicroL Parce que dans l'énoncé il est dit: une injection supplémentaire de 0.1MicroL ce qui me fait penser que je dois ajouter le 0,1 à une autre valeur
-
@anesthesiste
C'est bien une variation de volume.
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
@Noemi
Alors je trouve:
Sans bulles d'air: C=5.1030.1∗10−6\frac{5.10^3}{0.1*10^{-6}}0.1∗10−65.103=5∗1010Pa/m35*10^{10} Pa/m^35∗1010Pa/m3Avec bulles d'air: C=2000.1∗10−6\frac{200}{0.1*10^{-6}}0.1∗10−6200=2∗109Pa/m32*10^{9} Pa/m^32∗109Pa/m3
Je ne suis pas sûr des unités Pa/m^3
-
@anesthesiste
Tu n'as pas calculé la compliance mais l'élastance.
Vérifie la formule.
-
?Un Ancien Utilisateur dernière édition par

Alors il faut faire:
Sans bulles: 1/(5*10^10)
Avec bulles: 1/(2*10^9)
-
@anesthesiste
Tu peux faire ainsi. Mais tu aurais pu calculer directement ΔVΔP\dfrac {\Delta V}{\Delta P}ΔPΔV
-
?Un Ancien Utilisateur dernière édition par
en fait je ne vois pas comment car pour Delta V je ne vois quelles sont les valeurs
Est-ce que l'unité de la compliance dans les 2 cas est bien Pa/m^3?
-
@anesthesiste
L'élastance est en Pa/m3Pa/m^3Pa/m3,
La compliance en m3/Pam^3/Pam3/Pa
Sans bulles d'air : C=0,1×10−65×103=...C= \dfrac{0,1\times10^{-6}}{5\times10^3}= ...C=5×1030,1×10−6=...Attention, le volume est en litre en non en m3m^3m3.
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
Bonjour @Noemi,
Merci effectivement je trouve les mêmes valeurs avec les deux formules
Compliance sans bulles=2 * 10^-11 m^3/Pa
Compliance avec bulles =5 * 10^-10 m^3/Pa
-
?Un Ancien Utilisateur dernière édition par
Je dois aussi calculer la fréquence naturelle et le facteur d'amortissement du système en l'absence puis en présence de bulles d'air.
A l'inverse du calcul de la compliance je n'ai pas trouvé de formule que je pourrais appliquer. Est-ce qu'il y aurait peut-être des formules "générales"?Bon lundi
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur

J'ai trouvé ça mais je ne pense pas que ça s'adapte
-
@anesthesiste
Tu peux utiliser ses formules si tu connais CdC_dCd, LcL_cLc et RcR_cRc.
-
?Un Ancien Utilisateur dernière édition par
C'est ce que j'étais en train de parler avec un camarade. Il me dit de réutiliser Wn et £ en utilisant les valeurs trouvés précédemment mais ça me parait un peu trop simple.
J'essaie de faire des calculs
-
?Un Ancien Utilisateur dernière édition par
Après calculs je trouve:
Wn avec bulles: 4.47
Wn sans bulles: 22.36Facteur amortissement avec bulles: 0.56
Facteur amortissement sans bulles: 0.11
-
@anesthesiste
Les résultats sont corrects.
-
?Un Ancien Utilisateur dernière édition par
Merci Noemi.
Est ce que vu que se sont des fréquences je mets comme unité des Hertz?
-
@anesthesiste
Pour l'unité, vérifie à partir de l'unité de chaque terme.
-
?Un Ancien Utilisateur dernière édition par
Bonjour @Noemi et merci,
alors:
LC= PaS²/m3Pa S²/m^3PaS²/m3
Cd=m3/Pam^3/Pam3/Pa
Rc=PaS/m3Pa S/m^3PaS/m3Pour la fréquence d'oscillation: Pa s²/Pa?
Pour le facteur d'amortissement j'ai plus de mal
-
@anesthesiste
A partir des unités indiquées,
la fréquence d'oscillation est en S−1S^{-1}S−1.
et le facteur d'amortissement est sans unité.
-
?Un Ancien Utilisateur dernière édition par
Comment arrivez-vous à déterminer cela?
-
@anesthesiste
Tu utilises l'équation aux dimensions.
Pour la fréquence :
1PaS2m−3×m3Pa−1=1S2=1S=S−1\sqrt{\dfrac{1}{PaS^2m^{-3}\times m^3Pa^{-1}}}= \sqrt{\dfrac{1}{S^2}}=\dfrac{1}{S}=S^{-1}PaS2m−3×m3Pa−11=S21=S1=S−1
-
?Un Ancien Utilisateur dernière édition par
D'accord merci @Noemi je comprends comment faire
-
?Un Ancien Utilisateur dernière édition par
Ce message a été supprimé !
-
?Un Ancien Utilisateur dernière édition par
Ce message a été supprimé !
-
BBlack-Jack dernière édition par
@Noemi a dit dans Calcul d'inertance, de résistance et de compliance :
@anesthesiste
L'élastance est en Pa/m3Pa/m^3Pa/m3,
La compliance en m3/Pam^3/Pam3/Pa
Sans bulles d'air : C=0,1×10−65×103=...C= \dfrac{0,1\times10^{-6}}{5\times10^3}= ...C=5×1030,1×10−6=...Bonjour,
0,1 µL = 0,1 * 10^-6 * 10^-3 = 10^-10 m³
Et donc pour avoir C en Pa/m³ , c'est C = 10^-10/5000 = 2.10^-14 Pa/m³ (sans bulles d'air).
Enfin, c'est ce que j'aurais écrit.
-
?Un Ancien Utilisateur dernière édition par
Bonjour @Black-Jack ,
Oui c'est exact je l'avais corrigé par contre j'avais trouvé 2*10^-13
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
Non en fait vous avez raison j'ai fait une erreur de calcul par contre comme unité j'avais mis m^3/Pa
J'ai vérifié les calculs et je trouve donc:
2.10^-14 m^3/Pa sans bulles d'air
et
5.10^-13 m^3/Pa en présence de bulle
-
@anesthesiste
Les résultats sont corrects.
-
?Un Ancien Utilisateur dernière édition par
Merci @Noemi