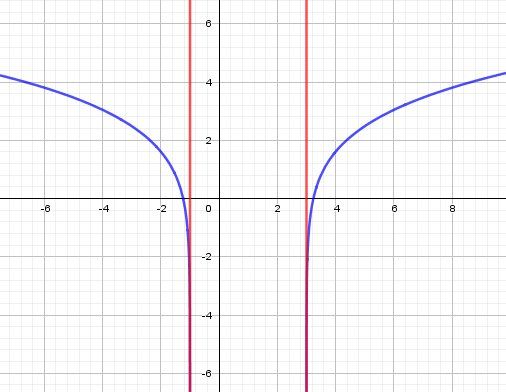
Limites fonction f(x)= ln(x^2-2x-3)

Bonjour,

J'ai un exercice qui me demande d'étudier les branches infinies de f(x)= ln(x^2-2x-3).
J'ai bien trouver Df= ] -l'inf;-1[ U ] 3;+l'inf[ . Je sais qu'il faut que j'étudie les limites aux bornes de Df. J'imagine que -1 et 3 sont asymptote verticale et -+l'inf horizontale mais j'ai du mal pour le calcul des limites.

Merci d'avance

@wassil-aidi , bonjour,

Oui pour $D_f$

Pistes pour les limites,

a) En $−∞-\infty$ et $+∞+\infty$ , la limite de $x^2-2x-3$ est la limite de son terme de plus fort degré donc de $x^2$ , donc + $∞\infty$

Vu que $lim⁡X→+∞ln(X)=+∞\displaystyle \lim_{X\to +\infty}ln(X)=+\infty$ , tu peux déduire que
$lim⁡x→∓∞f(x)=+∞\displaystyle \lim_{x\to \mp \infty}f(x)=+\infty$

Par contre, il n'y a pas d'asymptôte horizontale mais seulement une direction asymptotique qui est l'axe des abscisses
Si tu veux le justifier, tu dois prouver que
$lim⁡x→∓∞f(x)x=0\displaystyle \lim_{x\to \mp \infty}\dfrac{f(x)}{x}=0$

b) En $1)^-$ et en $3^+$ , en étudiant le signe de ( $x^2-2x-3$ ) , tu dois trouver que ( $x^2-2x-3$ ) tend vers $0^+$ donc le logarithme tend vers $−∞-\infty$

Les droites d'équations $x = - 1$ et $x = 3$ sont bien asymptôtes à la courbe.

Bons calculs.

Pour les limites en x→∓∞, je comprends que l'on garde seulement x^2, je trouve
lim ln (x^2)= +∞ mais à partir de la pourquoi je dois étudier lim f(x)/x ?
x→∓∞ x→∓∞
C'est une propriété ?

Et pour les limites en -1 et 3 sur Geogebra je rentre la fonction ln (x^2-2x-3) je ne trouve pas d'asymptote verticale malgré les résultats. C'est normal ?

Merci pour votre réponse

@wassil-aidi ,

Tout dépend de ton cours.
En $−∞-\infty$ et $+∞+\infty$ , tu parlais d'aymptôte horizontale : je t'ai répondu Non.
Il y a seulement une branche parabolique de direction symptotique l'axe des abscisses.
Si cela fait partie de ton cours, pour le justifier, tu prouves que la limite de $f(x)x\dfrac{f(x)}{x}$ est 0
Si ton cours n'en parle pas, tu ne fais rien
Je te mets un lien si ça t'interesse
https://www.mimaths.net/IMG/pdf/asymoblibranchparabol_p2_1415.pdf

Avec Geogegra, il faut que tu demandes le tracé des droites d'équations x=-1 et x=3 si tu veux les obtenir.

D'accord merci et oui dans mon cours il y a une formule lim ln(x)/x=0,

Merci pour votre aide

De rien, @wassil-aidi

Si tu veux justifier la direction asymptotique ( prouver que la limite de $f(x)x\dfrac{f(x)}{x}$ est 0), la propriété que tu indiques est utile mais elle n'est pas suffisante.

Tu dois transformer $f(x)x\dfrac{f(x)}{x}$

En $+∞+\infty$ ,
tu peux décomposer :
$f(x)x=ln[x2(1−2x−3x2)]x\dfrac{f(x)}{x}=\dfrac{ln\biggr[x^2(1-\dfrac{2}{x}-\dfrac{3}{x^2})\biggr]}{x}$

$f(x)x=ln(x2)x+ln(1−2x−3x2)x\dfrac{f(x)}{x}=\dfrac{ln(x^2)}{x}+\dfrac{ln(1-\dfrac{2}{x}-\dfrac{3}{x^2})}{x}$

$f(x)x=2ln(x)x+ln(1−2x−3x2)x\dfrac{f(x)}{x}=\dfrac{2ln(x)}{x}+\dfrac{ln(1-\dfrac{2}{x}-\dfrac{3}{x^2})}{x}$

La limite est $0 + 0 = 0$

En $−∞-\infty$ , tu peux indiquer que le comportement est le même , après avoir jusitifié que la droite d'équation $x = 1$ était axe de symétrie (car $f (1 - x) = f (1 + x)$ ).

Bon travail.

Inllustration : représentation graphique de la fonction (en bleu) et de ses deux asymptôtes "verticales" en rouge
ln(x^2-2x-3).jpg