Repèrage equation reduit
-
Papa Touré dernière édition par
Le plan est mini d'un repère orthonormé
ABC est un triangle.
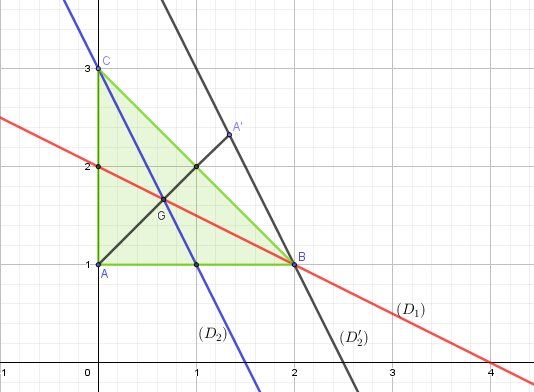
A(0,1),la mediane(D1) issue de B a pour equation y=-1/2x+2.
La mediane (D2) issue de c a pour equation y=-2x+3.
On cherche a partir de ses donnés de construire le triangle ABC c'est a dire a trouver les coordonnées de B et C.
1)Representer graphiquement les droites (D1) et (D2) et le point A.
2)trouver les coordonnées du centre de gravité G du triangle ABC.
3)A' est un point telque AG vecteur est égal GA' vecteur,trouver les coordonnées de A'.J'ai besoin d'aide svp
-
@Papa-Touré Bonjour (Marque de politesse à ne pas oublier !!)
Indique tes éléments de réponse et la question qui te pose problème.
As tu représenté les droites et placé le point A ?Calcule les coordonnées du point d'intersection des deux droites.
-
mtschoon dernière édition par

Bonjour,
@Papa-Touré , je te joins un schéma pour que tu puisses vérifier le tien
(D1) est en rouge
(D2) est en bleu
G est l'intersection des deux médianes c'est à dire le point d'intersection de (D1) avec (D2)
Vu que AG→=GA′→\overrightarrow{AG}=\overrightarrow{GA'}AG=GA′, G est le milieu de [AA']
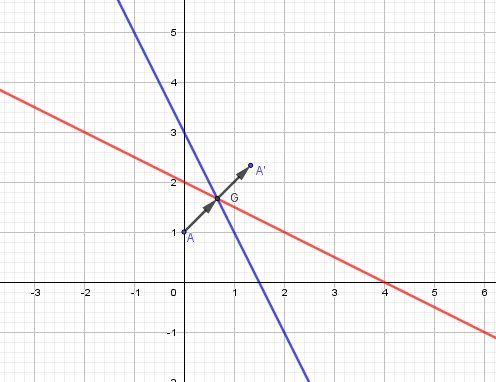
Tiens nous au courant de l'avancée de tes calculs, si tu le souhaites
-
Bonjour Papa-Touré et mtschoon,
@mtschoon a dit dans Repèrage equation reduit :
Bonjour,
@Papa-Touré , je te joins un schéma pour que tu puisses vérifier le tien
(D1) est en rouge
(D2) est en bleu
G est l'intersection des deux médianes c'est à dire le point d'intersection de (D1) avec (D2)
Vu que AG→=GA′→\overrightarrow{AG}=\overrightarrow{GA'}AG=GA′, G est le milieu de [AA']Il faudrait définir le point A′A'A′. Si A′A'A′ est le milieu du segment [BC][BC][BC], alors AG→=2GA′→\overrightarrow{AG}=2\overrightarrow{GA'}AG=2GA′. Le point A′A'A′ est donc mal placé.
-
mtschoon dernière édition par mtschoon

Bonjour,
Le schéma fait est la traduction fidèle de l'énoncé donné.
@Papa-Touré a écrit :
A' est un point telque AG vecteur est égal GA' vecteur,trouver les coordonnées de A'.@Papa-Touré a peut-être fait une faute en écrivant cette phrase...
Si c'est le cas, il le dira, s'il a besoin d'aide.
-
Papa Touré dernière édition par
@Noemi Bonjour
J'arrive vraiment pas a comprendre comment placer les pts ABC
-
As-tu déterminé les coordonnées du point G ?
A partir du graphique, tu peux en déduire B(2;1)B(2;1)B(2;1) et C(0;3)C(0;3)C(0;3).L'énoncé est-il complet ? pas de question 4) ?
-
Papa Touré dernière édition par
@Noemi
oui j'ai trouve les coordonnées de B et C.
Esk je peu determiné les coordonnées de G a partir de cette formule la xG=xa+xb+xc÷a+b+c
-
Le point GGG est le point d'intersection des deux droites.
Pour trouver l'abscisse du point GGG, tu résous −12x+2=−2x+3-\dfrac{1}{2}x+2=-2x+3−21x+2=−2x+3.
-
Papa Touré dernière édition par
@Noemi
J'ai trouvé x=⅔
-
C'est correct. Calcule l'ordonnée.
-
Papa Touré dernière édition par
@Noemi
J'ai remplacé x par sa valeur et j'ai trouvé 5/3
-
C'est correct.
-
Papa Touré dernière édition par
@Noemi
Merçi beaucoup.
-
mtschoon dernière édition par mtschoon

Bonjour,
Illustration graphique générale pour A,B,C,G pour consultation éventuelle.
(Je n'ai pas placé A' car je ne sais toujours pas si l'énoncé de @Papa-Touré relatif à A' était juste ou devait être modifié...)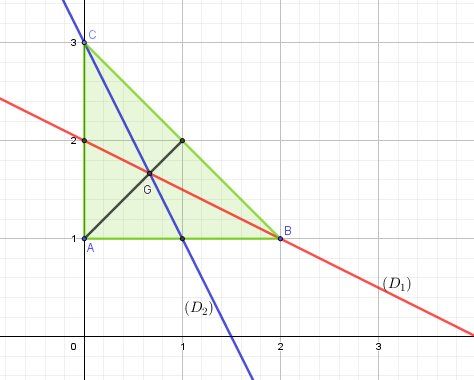
-
Papa Touré dernière édition par
@mtschoon Bonjour
J'ai d'autres questions.
c)A' est un pt telque AG=GA'; trouve les coordonnées de A'.
d)trouve une equation de la droite(D'2)qui passe par A' et qui est parallele a (D2).Pour la question c j'ai trouvé A'(1;2),
et j'ai representé (D'2 )1617910770512843181542.jpg
-
Si l'énoncé indique AG→=GA′→\overrightarrow{AG} = \overrightarrow{GA'}AG=GA′, il faut utiliser la première illustration graphique et en déduire les coordonnées du point A′A'A′ à partir des cordonnées des vecteurs.
Pour la question d) y=ax+by=ax+by=ax+b
Pour l'équation réduite de la droite (D'2), il faut déterminer le coefficient directeur aaa qui est le même que celui de la droite (D2).
Pour le calcul de l'ordonnée à l'origine bbb, il faut utiliser les coordonnées du point A′A'A′.
-
Papa Touré dernière édition par
@Noemi
J'ai utilisé cette formule xA'=xB+xC÷2 et yA'=yB+yc÷2 pour trouver les coordonnées de A'
-
D'après l'énoncé, le point A′A'A′ n'est pas le milieu du segment [BC][BC][BC] donc tu ne peux pas appliquer cette relation.
Tu peux appliquer cette relation pour le point GGG qui est le milieu du segment [AA′][AA'][AA′].
-
Papa Touré dernière édition par
@Noemi
Donc comment determiner les coordonnées de A'
-
A partir des coordonnées du point GGG.
Tu écris les relations
xG=xA+xA′2x_G=\dfrac{x_A+x_{A'}}{2}xG=2xA+xA′yG=yA+yA′2y_G=\dfrac{y_A+y_{A'}}{2}yG=2yA+yA′
Tu résous les équations pour déterminer les coordonnées du point A′A'A′.
-
Papa Touré dernière édition par
@Noemi
Pour xA' j'ai trouvé 4/3 et yA'=7/3
-
C'est correct.
-
Papa Touré dernière édition par
Ce message a été supprimé !
-
mtschoon dernière édition par mtschoon

Bonjour,
@Papa-Touré a dit dans Repèrage equation reduit (après mon second schéma) :
@mtschoon Bonjour
J'ai d'autres questions.
c)A' est un pt telque AG=GA'; trouve les coordonnées de A'.
d)trouve une equation de la droite(D'2)qui passe par A' et qui est parallèle a (D2).Au final, l'énoncé de @Papa-Touré était donc exact ! ! !
Donc A' a pour coordonnées (43,73)\dfrac{4}{3},\dfrac{7}{3})34,37)
Piste pour l'équation de (D2′)(D'_2)(D2′)
Deux droites parallèles ont même coefficient directeur , donc le coefficient directeur de (D2′)(D'_2)(D2′) est -2
L'équation réduite de (D2′)(D'_2)(D2′) est : y=−2x+by=-2x+by=−2x+b
Pour trouver b, on utilise les coordonnées de A' :
73=−2(43)+b\dfrac{7}{3}=-2(\dfrac{4}{3})+b37=−2(34)+bAprès calculs, on doit trouver b=5b=5b=5
L'équation réduite de (D2′)(D'_2)(D2′) est doncy=−2x+5\boxed{y=-2x+5}y=−2x+5
-
mtschoon dernière édition par mtschoon

-
Papa Touré dernière édition par Papa Touré
-
mtschoon dernière édition par

De rien @Papa-Touré ,
J'espère que pour toi tout est clair.
Bon dimanche !