Dérivée et courbe représentative

[Alexis Dedigama]

Bonjour à tous, j’aurais besoin d’aide pour cet exercice de maths s’il vous plait:

Scan supprimé par la modération.

[Noemi]

@Alexis-Dedigama Bonjour,

Le scan de l'énoncé du sujet est interdit sur ce forum. Seuls les graphiques, schémas ou figures sont autorisés.

Recopie l'énoncé et les questions de l'exercice.

Les réponses proposées sont fausses.

Le scan va être supprimé.

[Alexis Dedigama]

Énoncer: Soit f une fonction deux fois dérivable sur R. On note f’ sa dérivée et f’‘ sa dérivée seconde. La courbe représentative de la fonction dérivée est notée Cf’ est donné ci dessous.

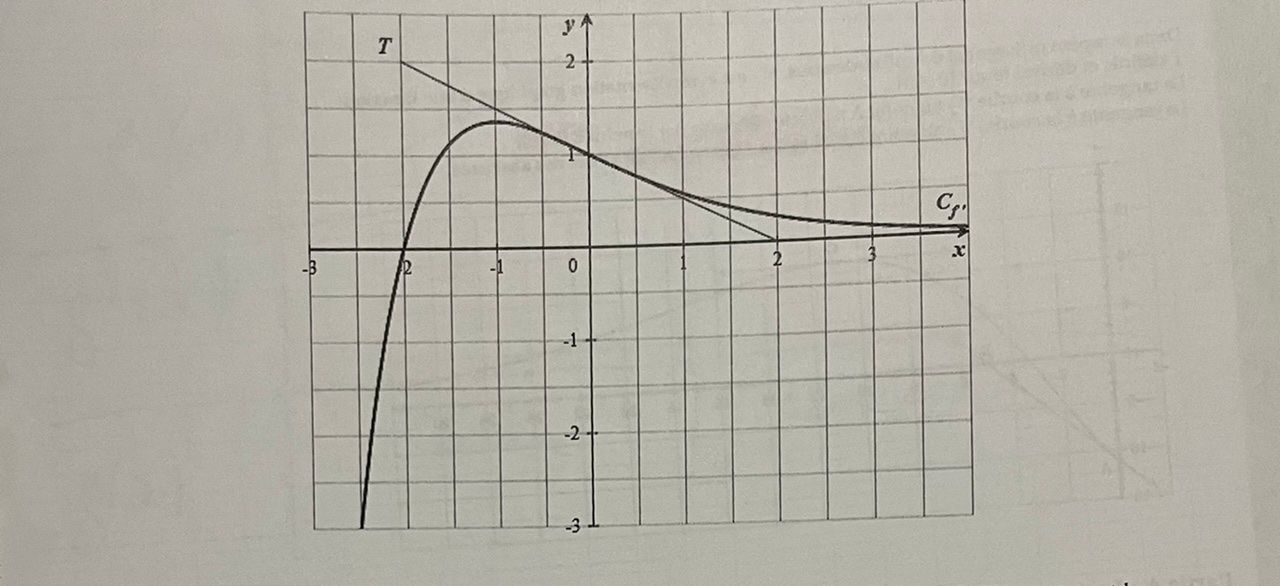
Une des quatre courbe C1, C2, C3, C4 ci-dessous est la courbe représentative de la fonction f et une autre est la courbe représentative de la dérivée seconde f’’.

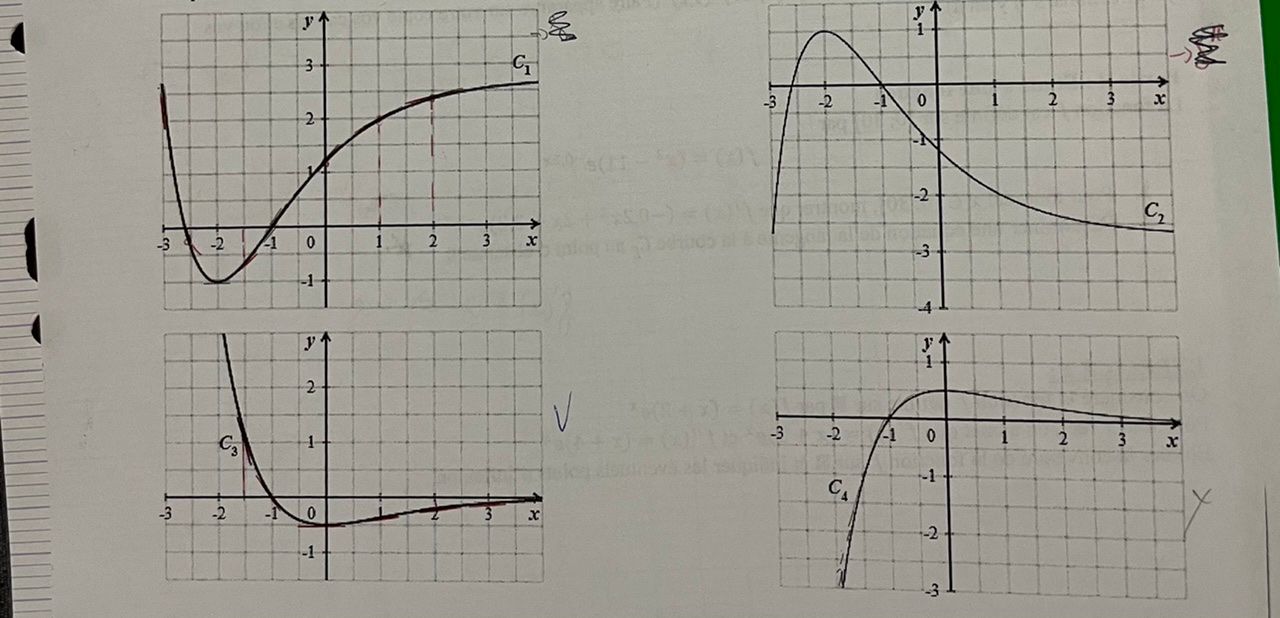
Déterminer la courbe qui représente f et celle qui représente f’’. Justifier

[mtschoon]

Bonjour,

@Alexis-Dedigama , observe les courbes.

Pistes,

a) Avec la courbe de f'

$f^{\prime }(x)>0$ pour $x>-2$ donc f croissante
$f^{\prime }(x)<0$ pour $x<-2$ donc f décroissante
$f^{\prime }(x)=0$ pour $x=-2$ donc minimum pour f

Cherche la fonction f satisfaisante

b) Avec la courbe de f'
$f^{\prime }$ croissante pour $x<-1$ donc $f^{\prime \prime }(x)>0$
$f^{\prime }$ décroissante pour $x>-1$ donc $f^{\prime \prime }(x)<0$
$f^{\prime }$ a son maximum pour $x=-1$ donc $f^{\prime \prime }(x)=0$

Cherche la fonction $f^{\prime \prime }$ satisfaisante

[Noemi]

Bonjour Alexis-Dedigama et mtschoom,

@mtschoon a dit dans Dérivée et courbe représentative :

Bonjour,

@Alexis-Dedigama , observe les courbes.

Pistes,

a) Avec la courbe de f'

$f^{\prime }(x)>0$ pour $x>2$ donc f croissante
$f^{\prime }(x)<0$ pour $x<2$ donc f décroissante
$f^{\prime }(x)=0$ pour $x=2$ donc maximum pour f

Cherche la fonction f satisfaisante

Attention, un signe $-$ oublié.
$f^{\prime }(x)<0$ si $x<-2$ donc fonction décroissante.
$f^{\prime }(x)>0$ si $x>-2$ donc fonction croissante.

$f^{\prime }(x)=0$ si $x=-2$ donc minimum pour $f$.

[mtschoon]

Merci Noemi
J'ai fait une mauvaise lecture .
J'ai rectifié

J'espère que @Alexis-Dedigama aura trouvé les "bonnes" courbes.