volume d'un pavé droit en fonction de x dans une pyramide

bonjour, j'ai un DM de math a rendre pour dans deux jours et je ne comprend pas la partie 2, la voici :

On considère une pyramide a base carrée de côté 10 cm et de hauteur 12 cm.
Dans cette pyramide est inscrit un pavé droit à base carrée. On voudrais trouver la hauteur du pavé droit correspondant à son volume maximal.
Soit x la hauteur du pavé droit et c la longueur du carré de sa base.

x prend ses valeurs dans un intervalle [a ; b].
Déterminer cet intervalle : l'intervalle est [0 ; 12]
on considère la fonction suivante qui permet de calculer le volume de pavé droit en fonction de sa hauteur x.
```
        1  def volume(x) :
        2         return x*(10-5/6*x)**2
```

justifier la formule de la ligne 2.

pouvez vous m'aider a justifier la formule de la ligne 2 s'il vous plait

@William-Griere Bonjour,

As-tu fait une figure ?
Pour calculer la mesure du côté de la base du pavé droit, tu peux appliquer la propriété de Thalès.
En posant longueur du côté de la base : 10 - 2a
$x12=a5\dfrac{x}{12}=\dfrac{a}{5}$
Tu déduis $a$ puis en utilisant la formule du volume d'un pavé droit tu en déduis la fonction indiquée.

merci pour votre aide et non je n'ai pas eu à faire de figure mais il y a tout de même une un shéma représentant un triangle rectangle BCO avec un rectangle DFOA à l'intérieur avec la longueur FO mesurant x et la longueur AO mesurant c/2

@William-Griere , bonjour,

Les scans d'énoncés ne sont pas autorisés, mais les scans de graphiques sont autorisés.

Pour plus de clarté, tu peux, si tu le souhaites, joindre la figure (seule).

Bonjour,

@William-Griere , quelques pistes complémentaires,

Tout d'abord, la formule de la ligne 2 est l'expression de V(x) qui est le volume du pavé droit à base carrée (en fonction de x).

Il faut donc que tu démontres que ce volume vaut :

$V(x)=x(10−56x)2\boxed{V(x)=x\biggr(10-\dfrac{5}{6} x\biggr)^2}$

Bien sûr, ce serait mieux d'avoir la figure donnée qui représente une portion (intérieure) de la pyramide et du pavé.
J'en mets une, mais j'ignore si les lettres sont au bon endroit.
Il faudra que tu adaptes.
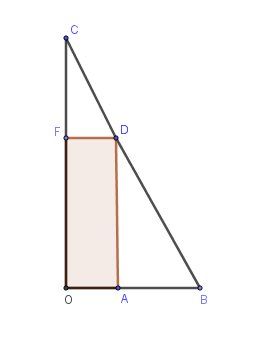
pavé.jpg

Dans mon schéma,
$O F = x$ (hauteur du pavé)
$O C = 12$ (hauteur de la pyramide)
$OA=c2OA=\dfrac{c}{2}$ ( demi longueur de la base carrée du pavé )
$O B = 5$ (demi-longueur de la base carrée de la pyramide)

Il faut que tu réalises ce que tout cela représente dans la figure en dimension 3 de la pyramide et du pavé.

Comme te l'a dit Noemi, tu utilises le théorème de Thalès

$OBFD=OCFC\dfrac{OB}{FD}=\dfrac{OC}{FC}$
Cela donne
$5c2=1212−x\dfrac{5}{\dfrac{c}{2}}=\dfrac{12}{12-x}$

Tu transformes cette égalité pour obtenir c en fonction de x

Après calculs, tu dois trouver :

$c=10−56xc=10-\dfrac{5}{6}x$

D'où

$V(x)=x×c2=....V(x)=x\times c^2=....$

Tu dois arriver à l'expression souhaitée.

Bons calculs et tiens nous au courant si besoin.