les vecteurs mathématiques
-
Livindiam Livin dernière édition par

bonjour
ABCD est un parallélogramme de centre O
E te F sont les points tels que AE= 2/3AD et BF=1/3BC
il faut démontrer que AE=FC
pouvez vous m'aidez s'il vout plait pour trouver FC
-
@Livindiam-Livin Bonjour,
Vu que le quadrilatère ABCDABCDABCD est un parallélogramme, AD→=BC→\overrightarrow{AD}=\overrightarrow{BC}AD=BC
de l'égalité BF→+FC→=BC→\overrightarrow{BF}+\overrightarrow{FC}=\overrightarrow{BC}BF+FC=BC,
tu déduis FC→\overrightarrow{FC}FC.Indique tes résultats si tu souhaites une vérification.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Livindiam-Livin , j'espère que tu as fait un schéma pour éclairer les calculs.
En voici un, si besoin.
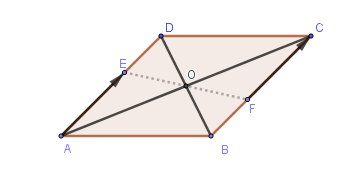
-
Livindiam Livin dernière édition par

@Noemi bonsoir
vu que BF= 1/3 et que BC = 3/3 , FC= 2/3
-
Livindiam Livin dernière édition par

@mtschoon bonsoir, dans l'exercice je dois faire un schéma
merci pour votre aide, c'est exactement ce que j'ai fais
-
Attention à l'écriture des vecteurs :
BF→=13BC→\overrightarrow{BF}=\dfrac{1}{3}\overrightarrow{BC}BF=31BC.
BC→=BF→+FC→\overrightarrow{BC}=\overrightarrow{BF}+\overrightarrow{FC}BC=BF+FC.
d'ou
FC→=23BC→\overrightarrow{FC}=\dfrac{2}{3}\overrightarrow{BC}FC=32BC.
-
Livindiam Livin dernière édition par

@Noemi merci !
il y a une seconde question que j'ai mal compris venant de ce meme exercice, puis je la poser ici ou dois-je réecrire l'énoncé ?
-
Si c'est le même exercice, pose la question ici.
-
Livindiam Livin dernière édition par

@Noemi comment en déduire que O, E et F sont alignés ?
-
Quelle est la nature du quadrilatère FCEAFCEAFCEA ?
-
mtschoon dernière édition par mtschoon

Bonjour,
@Livindiam-Livin , un complément si besoin.
J'espère que tu as terminé la démonstration de FC→=AE→\overrightarrow{FC}=\overrightarrow{AE}FC=AE
Pour la conséquence, je te conseille de compléter le schéma en traçant le quadrilataire AECF
Vu que FC→=AE→\overrightarrow{FC}=\overrightarrow{AE}FC=AE, ce quadrilatère est un parallélogramme (deux côtés opposés parallèles et de même longueur)
Dans un parallélogramme , les diagonales se coupent en leur milieu donc .... (tu termines le raisonnement).
-
mtschoon dernière édition par

Bonjour @Noemi ,
je ne t'ai pas vu connectée lorsque j'ai commencé à répondre...
-
Livindiam Livin dernière édition par

@mtschoon ici les diagonales sont EF et AC, donc elles se coupent en O donc O est le milieu de la diagonale EF
-
mtschoon dernière édition par

@Livindiam-Livin , oui , ton idée est bonne.
Il faudra l'exprimer un peu mieux, si tu peux.
O est le centre du parallélogramme ABCD donc le milieu de [AC]
[AC] et [EF] ayant même milieu (vu que AECF est un parallélogramme), le milieu de [EF] est O.
Donc E, O , F alignés.
-
Livindiam Livin dernière édition par

@mtschoon d'accord c'est plus clair, merci !
-
mtschoon dernière édition par

De rien @Livindiam-Livin
A+