Produit scalaire, quelqu'un peut-il m'aider à faire cet exercice,merci d'avance
-
EEdward R dernière édition par
Exercice 1:
On considere le carre ABCD ci-dessous. M est un point appartent a la diagonle [BD].
On note I le projete orthogonal de M sur (DC) et J le projete orthogonal de M sur [BC].
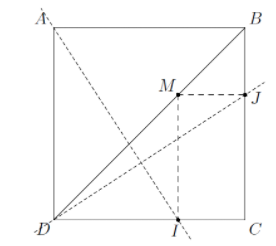
- Etablir la relation suivante: DI.DC=BC.JC
- En deduire que les droites (AI) et (DJ) sont perpendiculaires.

Pour 1, DI et DC sont 2 vecteurs de même direction et de même sens donc le produit scalaire = le produit des longueurs = |DI|.|DC| de même BC et JC or |DI| = |JC| = |IM| car DIM est 1 triangle rectangle isocèle et |BC| = |DC| = côté du carré.
Et pour le 2, on doit monter que DJ.AI=0, donc on fait
DJ.AI=(DC+CJ).(AD+DI)
=DC.AD+DC.DI+CJ.AD+CJ.DI (en vecteurs)
=0+DCDI-CJAD+0
=11/2-1/21=0 , donc DJ et AI sont perpendiculaires.
-
@Edward-R Bonsoir (Marque de politesse à ne pas oublier !!)
Une erreur question 2,
CJ→.AD→=−JC→.BC→\overrightarrow{CJ}.\overrightarrow{AD}=-\overrightarrow{JC}.\overrightarrow{BC}CJ.AD=−JC.BC
L'utilisation du résultat de la question 1 est suffisant pour conclure.
Si tu utilises des normes, précise que tu choisis DC= BC = 1.
-
EEdward R dernière édition par
merci beaucoup pour votre aide
-
BMMM dernière édition par
@Edward-R bonsoir, je sais que cela fait un moment que vous avez posté cet exo mais je voulais savoir d'où est-ce sur vous l'avez pris ? D'un manuel ou d'une autre source ? Merci d'avance si vous répondez
-
mtschoon dernière édition par

@BMMM , bonjour,
@Edward-R te répondra peut-être s'il repasse par là (?)...
Je ne peux pas te dire qu'elle est l'origine de cet énoncé , mais je peux de dire qu'il est conforme au programme de Première actuel.