Modèle de Verhulst- Etude de bactéries

Bonjour à tous j’ai un exercice à faire en maths, j’aimerais vraiment avoir de l’aide, je n’ai pas commencé parce que je comprends vraiment pas..
Je vous joins 2 documents que je ne peux pas écrire.

Énoncé:

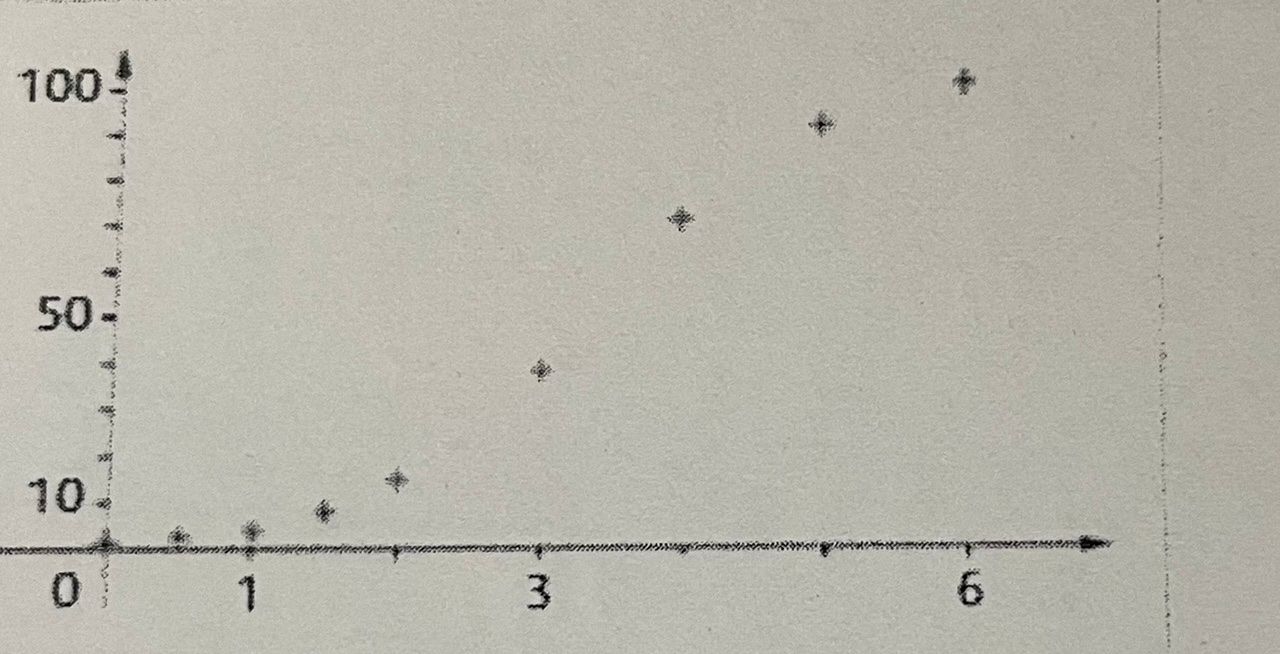
On étudie l’évolution d’une population de bactéries dans un milieu de culture. Le tableau ci-dessous donne l’évolution de cette population que l’on a représenté ci-contre par un nuage de points. Le temps « t » est exprimé en heure et le nombre de bactéries « N » en million.

On modélise l’évolution du nombre de bactéries sur les deux premières heures par la fonction f1 définie sur l’intervalle [0 ; 2] par f1(t)= e^1,4t

a. Déterminer le nombre réel a tel que f1 soit solution de l’équation différentielle y’= ay.

b. Justifier qu’au-delà de la deuxième heure cette modélisation donne une évolution trop rapide de la population de bactéries.

En 1938, Verhulst développe l’idée que, pour compenser une croissance devenue trop rapide, à partir d’un certain temps, le taux de croissance diminue au fur et à mesure que la population augmente. Il considère que le taux de croissance relatif sur l’intervalle [t ; t+h] est une fonction affine décroissante de la population au temps t. Ce qui se traduit ici, en notant f(t) le nombre de bactéries au temps t, par:

f(t+h) - f(t) / hf(t)= a - bf(t), avec a>0 et b>0

En faisant tendre h vers 0, on obtient que f est dérivable sur [0 ; +♾[ et solution de l’équation différentielle:
y’= ay-by^2
Pour la population de bactéries étudiée, on admet que a= 1,4 et b=0,014.
La fonction f est donc solution de l’équation différentielle (E): y’= 1,4y - 0,014y^2.

On considère g définie sur [0; +♾ [ par:
g(t)= 1/ f(t)

a. Calculer g(0) et montrer que g est solution de l’équation différentielle (E’):
y’= -1,4y + 0,014

b. Résoudre l’équation différentielle (E’) et montrer que, pour tout t ≥ 0, g(t)= 0,01 + 0,99e^ -1,4t.

c. En déduire que, pour tout t ≥ 0,
f(t)= 100/ 1+99e^-1,4t

d. Déterminer la limite de f en +♾ . Interpréter.

@Alexis-Dedigama , bonjour,

Piste pour démarrer,

1)a)
f_1(t)=e^{1.4t}$
$f_1'(t)=1.4e^{1.4t}$

$f_1$ solution de $y^{'} = a y$

c'est à dire : $f_1'(t)=af_1(t)$

$1.4e^{1.4t}=ae^{1.4t}$ tu en déduis la valeur de a.

Reposte si nécessaire.

@Alexis-Dedigama , un petit plus, si besoin.

1)a)J'espère que tu as trouvé $a = 1.4$

Pour le 1)b), tu calcules $f_1(t)$ pour t=3, 4, 5... et tu compares aux valeurs de N du tableau pour t=3, 4, 5...

Pour la 2)a) $f (0) = 1$ d'où $g(0)=11=1g(0)=\dfrac{1}{1}=1$

$g(t)=1f(t)g(t)=\dfrac{1}{f(t)}$ donc $g′(t)=−1(f(t))2f′(t)\boxed{ g'(t)=-\dfrac{1}{(f(t))^2}f'(t)}$

f est solution de l’équation différentielle (E'):
$y’= 1,4y - 0,014y^2$
donc
$f'(t)=1.4f(t)-0.014(f(t))^2$

Tu remplaces $f^{'} (t)$ par son expression en fonction de $f (t$ ) dans la formule encadrée qui donne $g^{'} (t)$
Tu simplifies et tu fais apparaître $g (t)$

Au final, tu dois trouver $g^{'} (t) = - 1.4 g (t) + 0.014$

Revois cela et essaie de poursuivre.

Bonsoir, premièrement merci beaucoup de m'avoir aidé !

Question 1.a)
f1(t)= e^1,4t
f'1(t)= 1,4e^t

f1 est solution de y'=ay, c'est-à-dire f'1(t)= af1(t)
1,4e^1,4t= ae^1,4t
1,4e^1,4t- e^1,4t= a
(Je barre les deux e^1,4t) donc a= 1,4

Question 1.b
Au delà de la deuxième heure, cette modélisation donne une évolution trop rapide de la population de bactéries.
-Calculons le nombre de bactéries pour t=3. f1(t)=e^1,43= 66,7
Donc il y a 66,7 (millions ?) de bactéries d'après cette modélisation alors que lorsqu'on regarde le tableau donné, au bout de 3heures il y a 37,9millions de bactéries
-Pour t=4. f1(t)=e^1,44= 270,4. Donc il y a 270,4 (millions ?) de bactéries d'après cette modélisation alors que lorsqu'on regarde le tableau donné, au bout de 4heures il y a 70,4millions de bactéries.
-Pour t=5. f1(t)=e^1,45=1096,6. Donc il y a 1096,6 (millions ?) de bactéries d'après cette modélisation alors que lorsqu'on regarde le tableau donné, au bout de 5heures il y a 90,1millions de bactéries
-Pour t=6. f1(t)+ e^1,46= 4447,1. Donc il y a 444,7 (millions ?) de bactéries d'après cette modélisation alors que lorsqu'on regarde le tableau donné, au bout de 6heures il y a 98millions de bactéries.
Cela montre bien une évolution trop rapide de la population de bactéries au-delà de la deuxième heure.

Question 2.a)

f(0)=1 (Je n'ai pas compris comment on le trouve ?) donc g(0)= 1/1=1
f est solution de l'équation différentielle (E) (C'est E' non ?) Et pourquoi parles-t-on de f car la question est ''montrer que g est solution de l'équation différentielle (E'): y'= -1,4y-0,0014y²''
Du coup y'= 1,4y-0,0014y² donc f'(t)= 1,4f(t)-0,014(f(t))² (pourquoi (f(t))² ?)
g'(t)= -1/(f(t))² (pq f((t))² ?) -1,4 f(t)-0,01(f(t))²
Je n'arrive pas à continuer...

@Alexis-Dedigama Bonsoir,

Pour la question 1 b.
Rajoute une ligne au tableau et calcule la valeur de N que tu compares avec l'évolution.

Pour la question 2
a) le tableau indique la valeur de f(0), N = 1.

$f$ est solution de l'équation différentielle $y'=1,4y-0,014y^2$ (E)
Comme $\dfrac{1}{g(t)}$ , alors $f′(t)=−g′(t)g(t)2f'(t)=-\dfrac{g'(t)}{g(t)^2}$
que tu remplaces dans l'équation différentielle pour trouver (E').

Bonjour,

@Alexis-Dedigama ,

Pour le 1)b), ce sont bien des millions de bactéries (tu as mis un point d'interrogation...)
Comme te l'indique Noemi, dispose avec un tableau comparatif pour ce ça soit plus lisible (une ligne pour t , une ligne pour N, une ligne pour $f_1(t)$ )

Pour le 2)a),

$f_1$ ,puis $f$ , modélisent l'évolution de la population de bactéries.
Donc, d'après le tableau donné, pour $t = 0$ , $N = 1$ donc nécessairement,on doit avoir $f_1(0)=f(0)=1$

Tu sembles avoir une difficulté sur $g^{'} (t)$

J'explicite une peu l'explication que je t'ai donnée précédemment .

Dans ton cours, tu dois avoir la dérivée du quotient de deux fonctions dérivables (avec dénominateur non nul)
En abrégé :
$(UV)′=U′V−UV′V2\biggr(\dfrac{U}{V}\biggr)'=\dfrac{U'V-UV'}{V^2}$
Si $U = 1$ , $U^{'} = 0$
Donc
$(1V)′=0′V−1V′V2=−V′V2\biggr(\dfrac{1}{V}\biggr)'=\dfrac{0'V-1V'}{V^2}=-\dfrac{V'}{V^2}$

La dérivée de $1f\dfrac{1}{f}$ vaut donc $−f′f2-\dfrac{f'}{f^2}$
Donc, comme déjà dit :
Vu que $g(t)=1f(t)g(t)=\dfrac{1}{f(t)}$ , $g′(t)=−f′(t)(f(t))2\boxed{g'(t)=-\dfrac{f'(t)}{(f(t))^2}}$

Tu sais que $f'(t)=1.4f(t)-0.014(f(t))^2$ (vu que f fest solution de $y’= 1,4y - 0,014y^2$ )

En remplaçant dans la formule encadrée :
$g′(t)=−1.4f(t)−0.014(f(t))2(f(t))2g'(t)=-\dfrac{1.4f(t)-0.014(f(t))^2}{(f(t))^2}$

Il te reste à simplifier le membre de droite par $f(t))^2$ et tu fais apparaître $g (t)$

c'est à dire :

$g′(t)=−1.4f(t)+0.014g'(t)=-\dfrac{1.4}{f(t)}+0.014$

$g′(t)=−1.4(1f(t))+0.014g'(t)=-1.4\biggr(\dfrac{1}{f(t)}\biggr)+0.014$

$g^{'} (t) = - 1.4 g (t) + 0.014$

Essaie de poursuivre et reposte si besoin.

Pour la 2.a je n’arrive vraiment pas à aller plus loin, et j’ai essayé de commencer la 2.b

@Alexis-Dedigama

Attention , c'est
$\times \dfrac{1}{f(t)}+0,014$
soit $\ g(t)+0,014$ ; Equation (E')

Pour la résolution,
Tu as trouvé le terme constant $0, 01$ .

Pour la résolution de l'équation sans second membre, soit $\ y(t)$ .
$y=ke^{-1,4t}$
soit $g(t) = ke^{-1,4t}+0,01$
Pour déterminer la valeur de $k$ utilise $g (0) = 1$ .

Mais du coup pour la 2.a comment je montre que g est solution de l’équation différentielle ? Et pour la question 2.b je n’ai pas compris comment trouver k et montrer que, pour tout t supérieur ou égale à 0, g(t)= 0,01 + 0,99 e^ -1,4t ?

@Alexis-Dedigama

Pour la question 2 a) tu as recopié la réponse donnée, mais celle-ci comporte une erreur de frappe.
Le $1, 4$ a été remplacé par $0, 4$ .
Donc vérifie et rectifie le calcul.

Pour le calcul de $k$
Résous l'équation
$1 = ke^0+0,01$

Ce message a été supprimé !

@Alexis-Dedigama

Oui remplace le $x$ par $t$ .

Attention à l'écriture le $0,0141,4\dfrac{0,014}{1,4}$ et le $0, 01$ ne sont pas en exposant

$g(t) = 0,01+ 0,99e^{-1,4t}$

Pour la question c. Exprime $\dfrac{1}{g(t)}$

Est-ce seulement ce que j’ai surligné en jaune que je dois remplacer par t ? Ou il y’a d’autres chose ? Et pour la c j’ai fait cela

@Alexis-Dedigama

Oui, et rectifie aussi le terme écrit à côté du $x$ ce n'est pas un exposant
Pour la question c ; il faut multiplier par 100, le numérateur et le dénominateur.

MERCI BEAUCOUP !!!!!!!! Et juste pour la dernière, comment faire ?

@Alexis-Dedigama

Pour la limite, si $t$ tend vers l'infini $e^{-1,4t}$ tend vers 0, donc $f (t)$ tend vers ....

Ce message a été supprimé !

@Alexis-Dedigama

L'expression de $f (t)$ est le résultat obtenu à la question c) soit :
$f(t)=1001+99e−1,4tf(t)=\dfrac{100}{1+99e^{-1,4t}}$

@Alexis-Dedigama

$f(t)=1001+99e−1,4tf(t)=\dfrac{100}{1+99e^{-1,4t}}$

la limite si $t$ tend vers l'infini est :
$1001+99×0=1001+0=100\dfrac{100}{1+99\times0}= \dfrac{100}{1+0}= 100$

Ce message a été supprimé !

@Alexis-Dedigama

C'est le nombre de bactéries en millions.

Merci, j’ai une dernière question, pour la question 2.b tous mes y je dois les remplacer par g ?

Pouvez vous relire mes questions 2.a, 2.b et 2.v svp ? Est-ce que j’ai mis g(t) au bon endroit ? Etc.. faut-il remplacer y(x) par g(t) dans toute ma résolution d’équation ?

Et en fait pour la 2.c toute la l’heure j’ai réussi mais maintenant je ne comprends plus pourquoi j’avais marqué f(t)= 1/ g(t)
f(t)= 1/ 0,01 + 99e^-1,4t. G(t) vaut 0,99e^-1,4t +0,01 et non 99e^-1,4t. Du coup je ne sais plus comment faire la c, si vous pouvez m’aider merci beaucoup et relire mes questions numéro 2 s’il vous plait.

@Alexis-Dedigama

C'est correct.

Pour la question c) j'ai indiqué la réponse dans un précédent post.
$\dfrac{1}{0,01+0,99e^{-1,4t}}$
en multipliant numérateur et dénominateur par 100,
$\dfrac{100}{1+99e^{-1,4t}}$

Merci beaucoup pour votre aide vraiment. Mais comment j’explique le fait d’avoir multiplier par 100 ? Pourquoi multiplier par 100 ? Certes je retrouve le même résultat, mais est-ce qu’il y a une explication ?

@Alexis-Dedigama

On multiplie par 100 pour trouver l'écriture demandée de la fonction.
On applique la règle : On ne change pas la valeur d'une fraction, si on multiplie par un même nombre son numérateur et son dénominateur.

@Alexis-Dedigama , bonjour,

Ce n'est vraiment pas sympathique pour les lecteurs qui viennent consulter, d'avoir effacer tous tes posts après avoir eu des aides, y compris l'énoncé ! ! !

@mtschoon a dit dans Modèle de Verhulst- Etude de bactéries :

@Alexis-Dedigama , bonjour,

Ce n'est vraiment pas sympatiques pour les lecteurs qui viennent consulter, d'avoir effacer tous tes posts après avoir eu des aides, y compris l'énoncé ! ! !

Bonjour,
Je suis évidemment du même avis ...
Le webmaster m'a déjà répondu que légalement, on ne peut pas empêcher quelqu'un de supprimer ses messages.

Une manière de contrer ce genre de comportement mesquin pourrait être, de systématiquement répondre en "Citant" le message auquel on répond ... et donc les messages supprimés par l'auteur resteraient visibles dans les réponses apportées.

Je suppose que cela n'est pas "illégal" et empêcherait les comportements comme ici.
... avec malheureusement une place plus grande d'espace mémoire nécessaire dans le site.

@Black-Jack a dit dans Modèle de Verhulst- Etude de bactéries :

Bonjour,
Je suis évidemment du même avis ...
Le webmaster m'a déjà répondu que légalement, on ne peut pas empêcher quelqu'un de supprimer ses messages.

Une manière de contrer ce genre de comportement mesquin pourrait être, de systématiquement répondre en "Citant" le message auquel on répond ... et donc les messages supprimés par l'auteur resteraient visibles dans les réponses apportées.

Je suppose que cela n'est pas "illégal" et empêcherait les comportements comme ici.
... avec malheureusement une place plus grande d'espace mémoire nécessaire dans le site.

Bonjour,
C'est un reflexe que je n'ai pas...mais l'idée est intéressante.
Bien sûr, cela alourdirait les topics et gênerait un peu la lecture des posts.
Faire cela, au moins pour conserver l'énoncé, serait une bonne chose.

De mémoire, sur l'ancien forum, cela ne se produisait pas.
Le système n'était pas le même et je suppose que le paramétrage était différent.

A suivre...

Bonne journée.

Bonjour à tous, je suis vraiment désolé d’avoir supprimé les messages mais le problème est que cet exercice est à rendre. J’ai posté mes résultats etc... et nous avons un groupe de classe, ils ont donc trouvé ce forum et ont partagé, cela me dérange, désolé encore, mais cela me dérange qu’ils envoient mon travail, un travail où j’ai mis du temp, pendant que les autres personnes de ma classe ne faisait rien... c’est trop facile pour eux, ils n’ont juste à recopier.

@Alexis-Dedigama , bonjour,

Merci d'avoir répondu.

Vu que ton souci est le "copiage", lorsque toi et tes camarades auront rendu le devoir à votre professeur, j'espère que tu penseras à restaurer les posts effacés (surtout l'énoncé) pour que ceux qui viennent consulter pour s'entraîner (et progresser dans leur formation) puissent le faire.

Bonjour,

Cel fait déjà 5 jours quz @Alexis-Dedigama a donné son explication...
Depuis, il n'a pas fait de restauration.
Je pense que la retauration n'aura pas lieu...

Raté... la restauration a bien eu lieu J’étais juste un peu chargé en ce moment.

@Alexis-Dedigama , bonsoir.

Je n'y croyais plus guère...

C'est super sympa, pour les consultants.

Un grand merci et à bientôt peut-être.

Remarque : Il suffisait de restaurer les posts effacés.

Il ne fallait absolument pas rajouter tes copies (mises dans un sens guère lisible... ), vu qu'elles n'y étaient pas précédemment et sur lesquelles les aidants n'ont donné aucun avis .

De plus, sur un forum, on tape au clavier ce que l'on souhaite...on ne joint pas de "copies-papier".

Pense-y une autre fois.

Bon travail !

Bonjour à vous j'ai besoin de vos aides un exercice de maths s'il-vous-plaît je peux mettre le sujet

@Love-Tyu , bonjour,

@Love-Tyu a dit dans Modèle de Verhulst- Etude de bactéries :

Bonjour à vous j'ai besoin de vos aides un exercice de maths s'il-vous-plaît je peux mettre le sujet

Bien sûr que tu peux.
Lorsque tu es connecté, tu choisis la bonne rubrique et tu cliques sur "Nouveau sujet"