algèbre sur les combinaisons permutation et autres

pouvez vous m'aider à trouver de combien de manières peut-on placer 10 billes dans deux poches différentes d'un vêtement ? s'il vous plaît

Bonjour,

Les billes sont-elles discernables (par exemple de couleur différentes) ou non ?

@Jack-Lundula Bonjour, (Marque de politesse à ne pas oublier !!)

Si les billes sont indiscernables, quels nombres de billes peut-on mettre dans une poche ?

@Jack-Lundula a dit dans algèbre sur les combinaisons permutation et autres :

pouvez vous m'aider à trouver de combien de manières peut-on placer 10 billes dans deux poches différentes d'un vêtement ? s'il vous plaît

Bonjour,

@Jack-Lundula ,

Toujours difficile de bien interpréter ce genre d'énoncé...
Tu n'as pas indiqué si les boules sont discernables ou pas...

Une piste possible dans les cas où les boules sont discernables

Par exemple :
Les boules sont numérotées de 1 à 10 : 1, 2, 3,...,10
Les poches s'appellent A et B.

Dans ce cas, le nombre de manières est $2^{10}=1024$

Explication :
Deux possibilites pour placer la boule 1
Lorsque la boule 1 est placée (dans A ou B), deux possibilites pour placer la boule 2
etc
etc.

Illustration avec un arbre de choix pour 3 boules (1, 2, 3) et deux poches (A et B).
(Avec les 10 boules , l'arbre serait...gigantesque...)

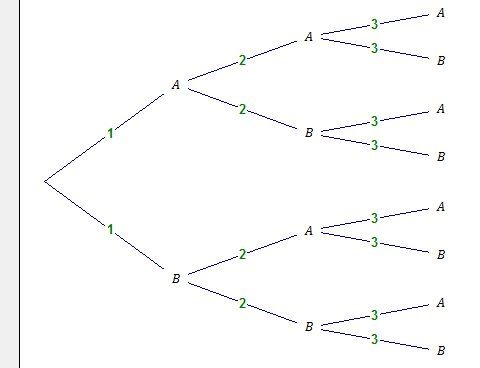
Il y a $2×2×2=23=82\times2\times 2=2^3=8$ chemins possibles.

Si on détaille ces 8 chemins (du haut du schéma vers le bas) :

1, 2, 3 dans A et aucun dans B
1,2 dans A et 3 dans B
1, 3 dans A et 2 dans B
1 dans A et 2, 3 dans B

2, 3 dans A et 1 dans B
2 dans A et 1, 3 dans B
3 dans A et 1, 2 dans B
aucun dans A et 1,2,3 dans B

Bonne réflexion

@Jack-Lundula , si tu préfères, avec les boules discernables, passer par les combinaisons, tu peux, mais c'est plus long.

Nombre de boules mises dans A, dans B, puis nombre de façons de le faire,tu obtiens :

A $\$ B $\$ nombre de façons**

0 10 $\$ $(100)\binom{10}{0}$

1 9 $\$ $(101)\binom{10}{1}$

2 8 $\$ $(102)\binom{10}{2}$

3 7 $\$ $(103)\binom{10}{3}$

4 6 $\$ $(104)\binom{10}{4}$

5 5 $\$ $(105)\binom{10}{5}$

6 4 $\$ $(106)\binom{10}{6}$

7 3 $\$ $(107)\binom{10}{7}$

8 2 $\$ $(108)\binom{10}{8}$

9 1 $\$ $(109)\binom{10}{9}$

10 0 $\$ $(1010)\binom{10}{10}$

En ajoutant ces 11 combinaisons et en utilisant la formule du binôme $a+b)^{n}$ , pour $a = 1$ , $b = 1$ et $n = 10$ $\$ tu obtiens le résultat cherché.

Remarque :
Si les boules sont indiscernables, tu peux utiliser cette démarche, mais ce sera bien plus rapide !

Tu peux regarder là :
http://villemin.gerard.free.fr/Denombre/aaaBalle/Balle01.htm