Microéconomie : Productivité marginale
-
Rémy E dernière édition par Rémy E
Bonjour,
La fonction d'une entreprise dépendante dépendante uniquement du nombre d'employé (L) est :
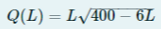
oû Q est la quantité produite (en milliers d'unités)Si initialement vous avez 5 employés, trouvez la productivité marginale du travail-
Q(L) = 18.46 (or je ne sais comment trouver cette réponse)Merci d'avance.
-
@Rémy-Eperon Bonjour (Marque de politesse à ne pas oublier !!)
Quelle relation y a t-il entre la productivité marginale et la fonction de production d'une entreprise ?
-
Rémy E dernière édition par Rémy E
Bonjour @Noemi La productivité marginale désigne le gain qu'on fait en produisant à chaque fois une unité de plus. A mon avis, il faut ici dériver la fonction pour trouver cette variation.
-
@Rémy-Eperon
Oui, dérive la fonction et calcule Q′(5)Q'(5)Q′(5).
La dérivée est : Q′(L)=400−6L−3L400−6LQ'(L)=\sqrt{400-6L}-\dfrac{3L}{\sqrt{400-6L}}Q′(L)=400−6L−400−6L3L
-
Rémy E dernière édition par
@Noemi Merci beaucoup ! Effectivement on trouve 18.46...
Cependant pourriez-vous me spécifier comment vous avez trouver cette dérivée, car je n'avais pas trouvé la même…
-
Indique ton calcul.
C'est de la forme U×VU \times VU×V.
-
Rémy E dernière édition par
@Noemi Je ne comprends pas la deuxième partie, comment la trouver…
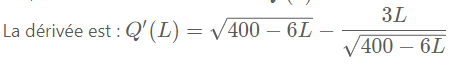
-
La dérivée de 400−6L\sqrt{400-6L}400−6L est −62(400−6L)\dfrac{-6}{2(\sqrt{400-6L})}2(400−6L)−6
-
Rémy E dernière édition par
@Noemi Ce que vous m'aviez initialement donné était juste ! Car cela me donnait le bon résultat, cependant je ne savais pas comment dériver ma fonction première et aurais voulu une précision quant à cela.
La fonction de base était :
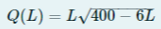
-
Pose : U=LU=LU=L, soit U′=...U'= ...U′=...
et V=400−6LV=\sqrt{400-6L}V=400−6L, soit V′=...V'=...V′=...
Puis : (U×V)′=U′V+UV′(U\times V)'=U'V + UV'(U×V)′=U′V+UV′
-
Rémy E dernière édition par
@Noemi D'accord c'est tout bon. Merci encore !