Primitives et équations différentielles
-
Kenza Beloudi 1 juin 2021, 17:51 dernière édition par
Bonsoir, j’ai 4 exos de maths à faire. J’ai écris les énoncés sur les feuilles et mes réponses, j’aimerai une correction.
Merci d’avance. Ps: je galère pour l’exo 4 question 3.Exo 1 et exo 2:
Exo 3:
Exo 4:
-
@Kenza-Beloudi Bonsoir,
Un seul exercice par post et l'énoncé est à écrire.
Exercice 3, la conversion de 2h30 minutes en minutes est fausse.
L'exercice 4 est à revoir des le début.
-
Kenza Beloudi 1 juin 2021, 19:25 dernière édition par
Oui j’ai remarqué plus tard pour la conversion de 2h30. Pouvez vous me donner des pistes pour l’exercice 4 svp car je savais que je ne l’avais pas réussi
-
Commence par résoudre la première équation.
-
Kenza Beloudi 1 juin 2021, 19:33 dernière édition par
Ke^2x + 4
-
Une erreur de signe.
y=ke2x−4y= ke^{2x}-4y=ke2x−4Applique le même raisonnement pour la deuxième équation.
Solution particulière : ....
Solution ....
-
Kenza Beloudi 1 juin 2021, 21:11 dernière édition par
C’est bon j’ai réussi merci j’aimerais juste de l’aide sur la dernière équation svp
-
Kenza Beloudi 1 juin 2021, 21:43 dernière édition par
Montrer que la fonction f definie sur R par
f(x)=(x+1)e^-2x est solution de l’équation différentielle (E): y’ + 2y= e^-2x. Je sais qu’il faut dérivér f(x).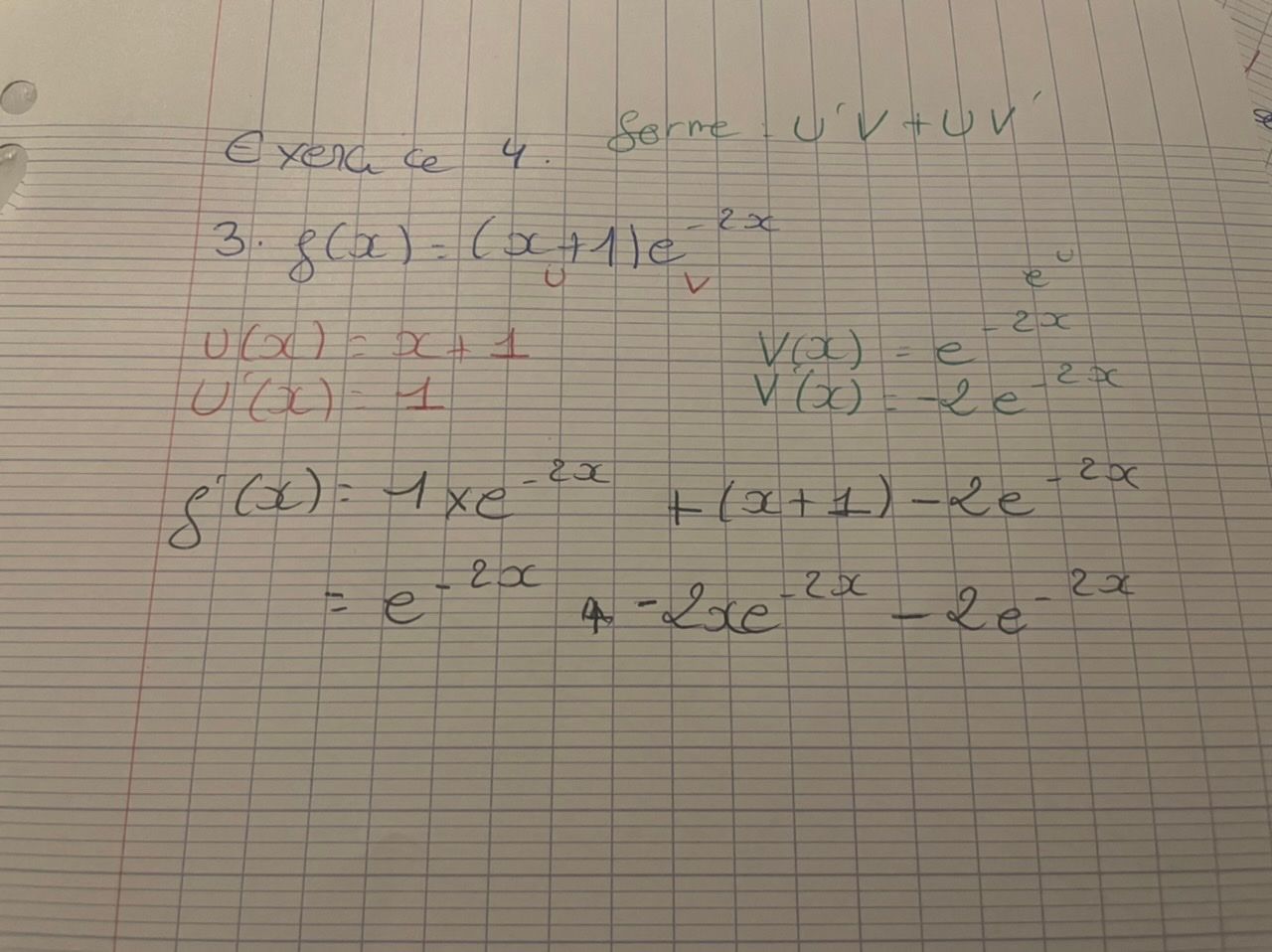
-
Attention à la rédaction. Tu peux simplifier et factoriser.
f(x)=(x+1)e−2xf(x)= (x+1)e^{-2x}f(x)=(x+1)e−2x
f′(x)=1×e−2x+(x+1)×(−2e−2x)f'(x)= 1\times e^{-2x}+(x+1)\times (-2e^{-2x})f′(x)=1×e−2x+(x+1)×(−2e−2x)
f′(x)=e−2x−2xe−2x−2e−2xf'(x)=e^{-2x}-2xe^{-2x}-2e^{-2x}f′(x)=e−2x−2xe−2x−2e−2x
f′(x)=−e−2x−2xe−2xf'(x)= -e^{-2x}-2xe^{-2x}f′(x)=−e−2x−2xe−2x
f′(x)=−(1+2x)e−2xf'(x)=-(1+2x)e^{-2x}f′(x)=−(1+2x)e−2x