probabilité de l1 bonjour j'ai besoin d'aide urgent

[camille567888]

Afin de tester l'efficacité d'un médicament contre le cholestérol, des patients nécessitant d'être traités ont accepté de participer à l'essai clinique d'un laboratoire. Dans cet essai, 70%
des patients ont pris le médicament pendant un mois, les autres ayant pris un placebo.
On étudie la baisse du taux de cholestérol après l'expérimentation. On constate une baisse de ce taux chez 75%
des patients ayant pris le médicament, et aucune baisse pour 88%
des personnes ayant pris le placebo.
On choisit au hasard une personne ayant participé à l'expérimentation. Calculer la probabilité que son taux de cholestérol ait baissé. On donnera deux chiffres après la virgule.

Question 2
Texte de la question
Suite de la question précédente.
On choisit au hasard une personne dont le taux de cholestérol a baissé à l'issue de l'expérimentation.
Calculer la probabilité qu'elle ait pris le médicament. On donnera deux chiffres après la virgule.

Question 3
Texte de la question
La laboratoire annonce que 17% des patients utilisant le médicament présentent des effets secondaires. On choisit au hasard et de façon indépendante 215 personnes traitées par ce médicament et on note S la variable aléatoire représentant le nombre de personnes présentant des effets secondaires.
Parmi les assertions suivantes, lesquelles sont vraies ?
Veuillez choisir au moins une réponse :
a. S suit la loi binomiale de paramètres 215 et 0,17
b. La probabilité qu'au moins une personne présente des effets secondaires est proche de 0,3
c. L'écart-type de S vaut environ 5,51
d. S suit la loi binomiale de paramètres 215 et 3655
e. S suit la loi de Bernoulli de paramètre 0,17
f. La probabilité qu'au moins une personne présente des effets secondaires est proche de 1
g. S suit la loi de Bernoulli de paramètre 3655
h. La variance de S vaut environ 30,34

[Noemi]

@camille567888 Bonjour,

Indique tes éléments de réponse et la question qui te pose problème.

[mtschoon]

Bonjour,

@camille567888 , je te conseille de faire un arbre pour démarrer ton exercice (Première question).
Si nécessaire, je t'en joins un.
Notations utilisées :
M pour "médicament "
P pour "Placebo"
B pour" baisse"
$\overline{B}$ pour "non baisse"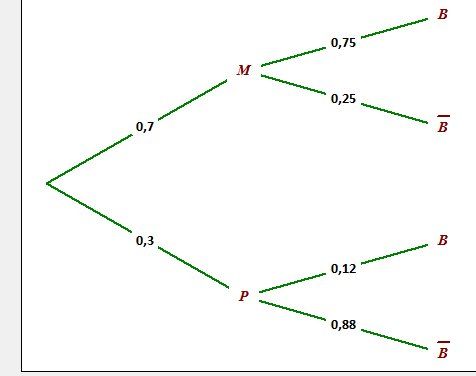

Tu dois donc chercher $p(B)$, avec l'arbre.

$p(B)=(0.7\times 0.75)+(0.3\times 0.12)=...$

Pour la question 2, tu dois calculer

$p_B(M)=\frac{p(B\cap M)}{p(B)}=...$

Essaie de poursuivre et reposte si besoin.