diargramme de venn et ensembles
-
Lloicstephan dernière édition par
bonjour j'ai ici iun petit exo qui me tracasse
dans un groupe de personne, 189 sont sportivifs 105 sont fumeur 42 sont les deux et 63 sont ni l'un ni l'autre.
1- combien de personne compose le groupe
2- quel est le nombre de sportif non fueursperso pour la premiere je pense a 189+105+63-42
pou la deuxieme question je pense a 105-42
merci de m'eclairer
-
@loicstephan Bonjour,
C'est correct pour la question 1. La question 2 est à vérifier.
-
Lloicstephan dernière édition par
pour la questin 2 j'ai fait exactement (189+105+63-42)-63-105
-
Question 2 : C'est correct, tu peux écrire : 189 - 42 = ....
-
BBlack-Jack dernière édition par
Bonjour,
L'exercice est intitulé Diagramme de Venn
Je présume donc que tu devais résoudre ton problème en utilisant un diagramme de Venn.
Là tu fais ainsi ?
-
Lloicstephan dernière édition par
@Black-Jack
bon mais je amitrise pas les proprietes
-
Le schéma avec les pointillés à compléter.
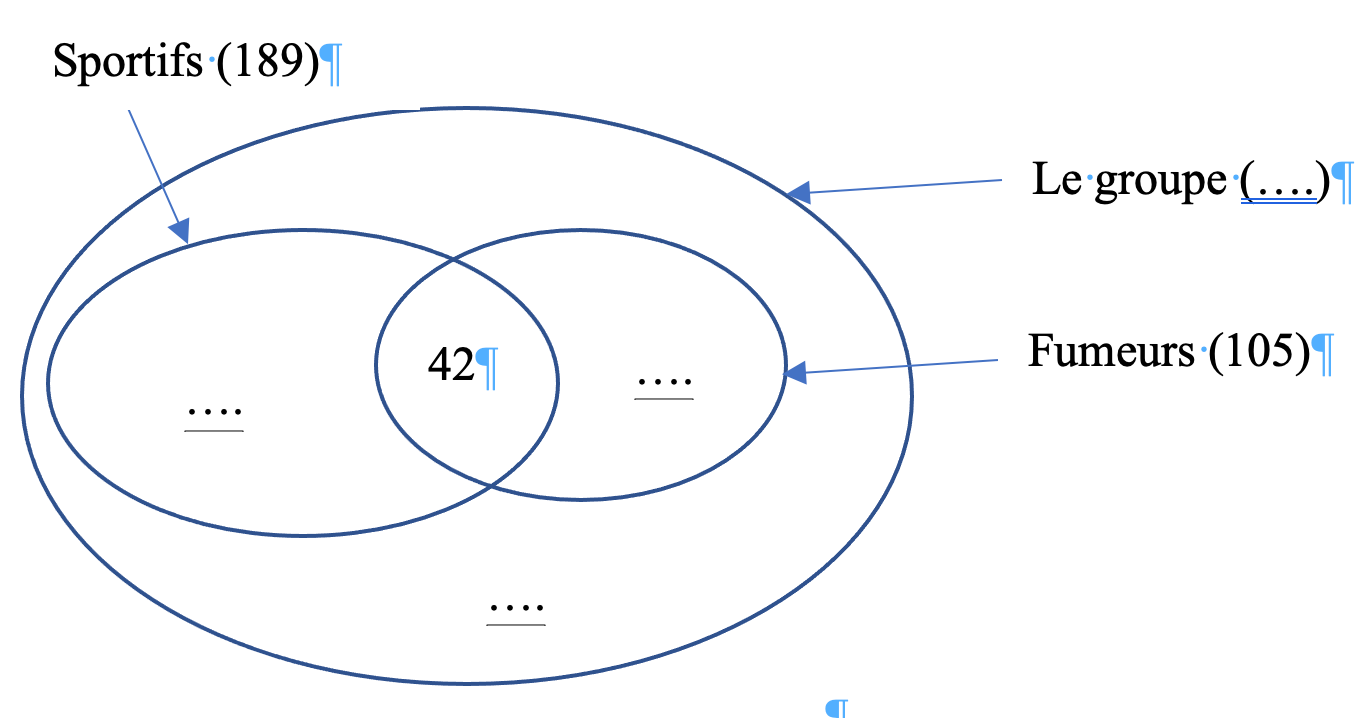
-
Lloicstephan dernière édition par
@Noemi
oui ce digramme la je l'avais deja dessiner pour trouver le total je me suis appuyer su l'axiome totale de probabilite
suposon q'on avait au depart un nombre total defini? le vrai total serait toujours retranche de l'intesection?
-
Pour calculer le nombre total de personnes, tu peux additionner les nombres inscrits dans le diagramme.
Le nombre de sportifs non fumeurs est juste une lecture du diagramme.
-
Lloicstephan dernière édition par
@Noemi on ne se compend pas madame je dis ceci: si un total avait deja ete defini le vrai total serait toujour retranché de l'intersection?car
a la question le total de personne est bien 189+105+63-42 ? je ais poster l'exercic en question et vous verrez ce que je dis !
-
Le calcul indiqué est juste. J'ai indiqué dans mes premières réponses que ton résultat était exact.
J'ai juste proposé une méthode de résolution des deux questions utilisant le diagramme de Venn. On trouve les mêmes résultats.
-
Lloicstephan dernière édition par
@Noemi
je demande que la formule (189+105+63-42) correspond a quoi ? telle est ma preoccupation car j'ai un autre excice ou un total est donné au depart je l'ai deja poste l'exercice lancez y un coup d'oeil s'il vous plait merci
-
Ce calcul correspond au nombre de personnes du groupe.
-
mtschoon dernière édition par mtschoon

Bonjour,
@loicstephan a dit dans diargramme de venn et ensembles :
bon mais je ne maitrise pas les propriétés
@loicstephan , effectivement, il serait bon d'expliciter les calculs en utilisant les propriétés usuelles.
Je détaille un peu ces propriétés, si besoin.
S'il s'agit d'un devoir , tu ne peux pas te contenter de faire du "numérique",
Il faut expliciter le raisonnement correctement, il me semble.Le nombre d'éléments d'un ensemble fini s'appelle son cardinal (cardcardcard en abrévation)
NOTATIONS :
Soit GGG l'ensemble des personnes du groupe
Soit SSS l'ensemble des sportifs : card(S)=189card(S)=189card(S)=189
Soit FFF l'ensemble des fumeurs : card(F)=105card(F)=105card(F)=105
Soit S∩FS\cap FS∩F l'ensembles des personnes, à la fois sportives et fumeuses : card(S∩G)=42card(S\cap G)=42card(S∩G)=42
L'ensembles des personnes sportives ou fumeuses est S∪FS\cup FS∪F
("ou" est au sens inclusif)
L'ensemble des personnes non sportives et non fumeuses est le complémentaire de (S∪F)S\cup F)S∪F) dans E.
On le note CG(S∪F)C_G(S\cup F)CG(S∪F) ou S∪F‾\overline{S\cup F}S∪F : card(S∪F‾)=63card(\overline{S\cup F})=63card(S∪F)=63CALCULS en respectant l'ordre des questions :
1)
card(S∪F)=card(S)+card(F)−card(S∩F)=189+105−42=252card(S\cup F)=card(S)+card(F)-card(S\cap F)=189+105-42=252card(S∪F)=card(S)+card(F)−card(S∩F)=189+105−42=252
Card(G)=card(S∪F)+card(S∪F‾)=252+63=...Card(G)=card(S\cup F)+card(\overline{S\cup F})=252+63=...Card(G)=card(S∪F)+card(S∪F)=252+63=...
2)
Sportifs non fumeurs : card(S card(S\ card(S \ S∩F)=cardS−card(S∩F)=189−42=147\ S\cap F)=card S - card (S\cap F)=189-42=147 S∩F)=cardS−card(S∩F)=189−42=147REMARQUE :
Autre façon (qui te permet de compléter le diagramme de Venn au fur et à mesure des calculs, mais qui ne respecte pas l'ordre des questions, donc ce n'est pas la méthode attendue par l'énoncé) :
partionner SUFSUFSUF en 3 parties disjointes :Sportifs non fumeurs : card(Scard(Scard(S \ S∩F)=cardS−card(S∩F)=189−42=147S\cap F)=card S - card (S\cap F)=189-42=147S∩F)=cardS−card(S∩F)=189−42=147
Fumeurs non sportifs : card(Fcard(Fcard(F \ S∩F)=cardF−card(S∩F)=105−42=63S\cap F)=card F - card (S\cap F)=105-42=63S∩F)=cardF−card(S∩F)=105−42=63
A la fois Sportifs et Fumeurs : card(S∩G)=42card(S\cap G)=42card(S∩G)=42
La somme des 3 te donne card(S∪F)=252card(S\cup F)=252card(S∪F)=252, puis card(G)=card(S∪F)+card(S∪F‾)=...card(G)=card(S\cup F)+card(\overline{S\cup F})= ...card(G)=card(S∪F)+card(S∪F)=...
-
Lloicstephan dernière édition par
@mtschoon
merci bien pour ces proprietes
-
mtschoon dernière édition par

@loicstephan, de rien !
Tu peux faire de même pour le second exercice qui est mieux organisé.
Dans le second exercice sur ce sujet, en suivant l'ordre des questions, on complète le diagramme de Venn logiquement ( ce qui n'est pas le cas de celui-ci).