Diagramme de venn 2 moins comprehensible
-
Lloicstephan dernière édition par Noemi
Un centre de loisir acceuille 100 enfants. deux sports sont proposés: le football et le tenis.
on remarque que 60 enfants aiment le football, 45 enfants aiment le tennis et 18 enfants aiment le football et le tennis .
a-determiner le nombre d'enfant qui aieent le football san aimer le tennis
b-determiner le nombre d'enfant qui aiment le tennis sans aimer le football
c- determiner le ombre d'enfant qui aiment le tennis ou le football
d-determiner le nombre d'enfant qui aiment aucun des deux sportperso si le total 100 reprensenten quoi et (60+45-18) represent quoi ?
-
@loicstephan Bonsoir (Marque de politesse à ne pas oublier !!)
Propose le diagramme de Venn.
-
Lloicstephan dernière édition par
@Noemi desole madame pour la marque de politesse comme il s'agissait du continuite j'ai pas voulu reprendre desole quant au diagramme de venn je sais pas comment le construire ici !
-
Lloicstephan dernière édition par
en procedant de la meme maniere 87 persone constitu le groupe 60+45-18
pour le a : 87-45
pour le b: 87-60
pour le c : 87
-
Complète le diagramme :
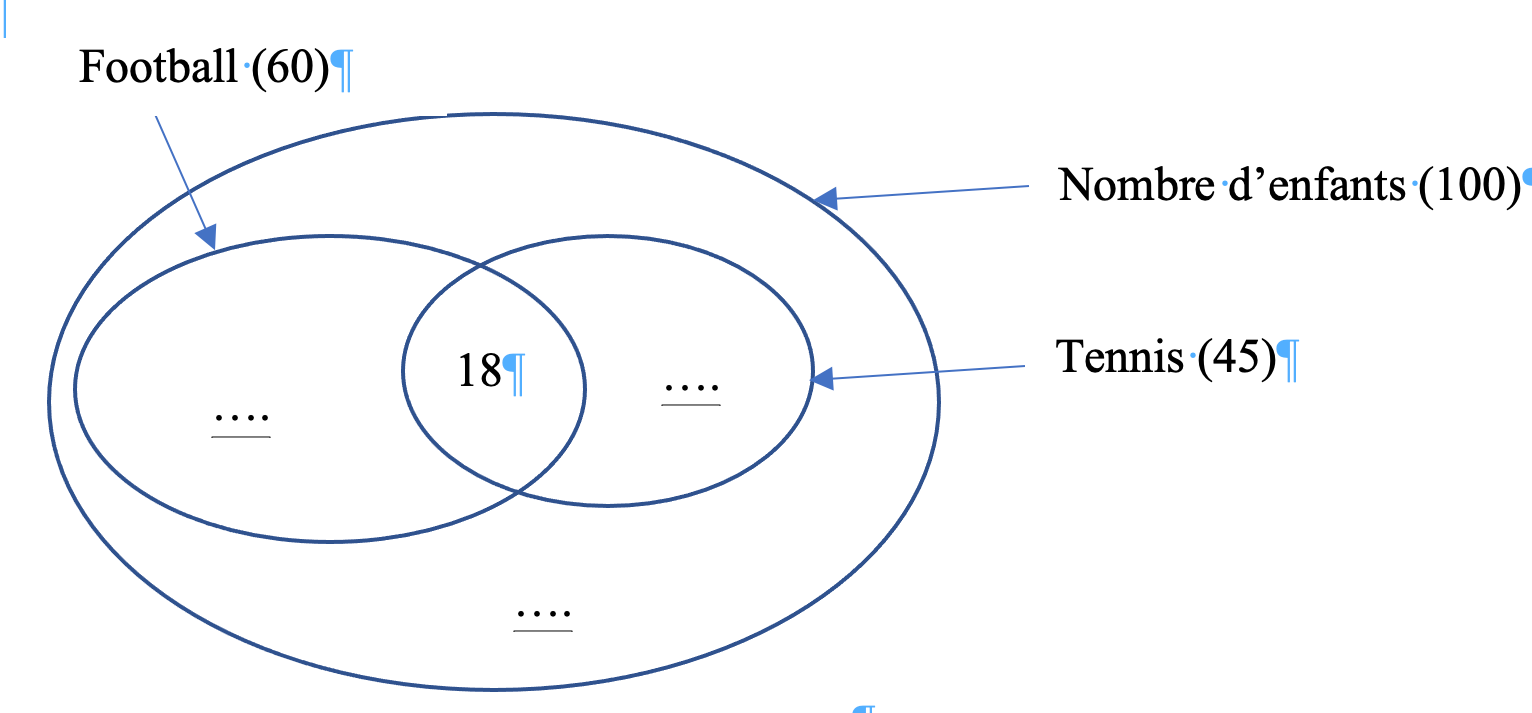
-
Lloicstephan dernière édition par loicstephan
@Noemi si le groupe ici est 100 dans ce ce cas le calcul precedent correspond a quoi? a la question c?
sinon lareponse c serait negative 100-45-60si le groupe est 100
a- 100-45
b-: 100+60
-
Lloicstephan dernière édition par
un autre raisonnement est si le groupe est 100 ainsi
60+45-18=87 : qui represente la question c la question d est obtenue enfaisint le groupe 100-87=13
-
En complétant le diagramme, tu obtiens rapidement la réponse à chacune des questions.
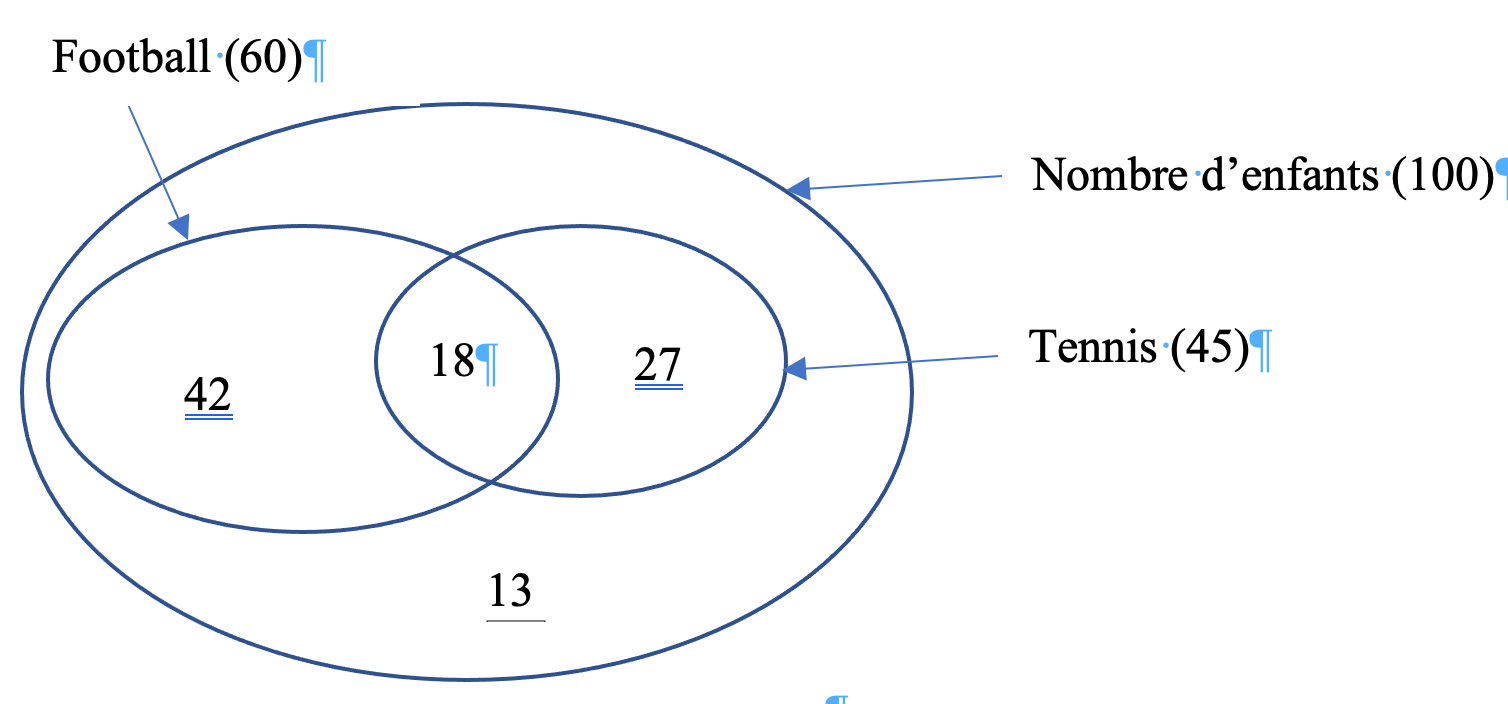
a- 42
....
Je te laisse proposer tes réponses.
-
mtschoon dernière édition par mtschoon

Bonjour,
@loicstephan , au final, tu as eu toutes les réponses.
En complément éventuel, je t'indique ls notations/formules que tu as dû utiliser.
GGG : Groupe ; card(G)=100card(G)=100card(G)=100
FFF : Football ; car(F)=60car(F)=60car(F)=60
TTT: Tennis : card(T)=45card(T)=45card(T)=45
card(T∩F)=18card(T\cap F)=18card(T∩F)=18a) card(Fcard(Fcard(F \ F∩T)F\cap T)F∩T)=card(F)−card(F∩T)card(F)-card(F\cap T)card(F)−card(F∩T)
b) card(Tcard(Tcard(T \ T∩T)\ T\cap T) T∩T)=card(T)−card(F∩T)card(T)-card(F\cap T)card(T)−card(F∩T)
c) card(F∪T)=card(F)+card(T)−card(F∩T)card(F\cup T)=card(F)+card(T)-card(F\cap T)card(F∪T)=card(F)+card(T)−card(F∩T)
d) card(F∪T‾)=card(G)−card(F∪T)card(\overline{F\cup T})=card(G)-card(F\cup T)card(F∪T)=card(G)−card(F∪T)
-
mtschoon dernière édition par

@loicstephan , une remarque relative à la différence de deux ensembles (qui doit être expliquée dans ton cours)
Soit A et B deux ensembles.
Le différence AAA \ BBB parfois notée plus simplement AAA - BBB est l'ensemble des éléments appartenant à AAA mais n'appartenant pas à BBBDonc
AAA \ BBB = AAA \ A∩BA\cap BA∩B
card(Acard(Acard(A \ BBB )=card(A)card(A)card(A) - card(A∩B)card(A\cap B)card(A∩B)Dans mes indications, j'aurais pu utiliser AAA \ BBB mais j'ai trouvé pour clair d'utiliser AAA \ A∩BA\cap BA∩B
Bonnes réflexions.