Trouver l'équation d'une fonction racine carré a partir de points situé sur un graphique
-
Jérémie Obsomer dernière édition par Noemi
Bonjour,
Je bloque un peu sur la résolution d'un exercice que l'on m'a posé, calculer à partir du graphe d'une fonction racine carré, son équation. Auriez-vous s'il vous plait la possibilité de m'éclairer a ce sujet ?
Bien à vous et au plaisir de pouvoir lire vos réponses
Merci d'avance
-
mtschoon dernière édition par

@Jérémie-Obsomer , bonjour,
Ce serait mieux d'écrire l'énoncé exact de ton exercice, car ce que tu indiques manque de précision.
La fonction "racine carrée" est la fonction qui, à tout x positif (x≥0x \ge 0x≥0) fait correspondre x\sqrt xx : f(x)=x\boxed{f(x)=\sqrt x}f(x)=x
(c'est ainsi en France)Il serait bon que tu précises l'expression des "fonctions racines carrées" dont tu parles.
-
Jérémie Obsomer dernière édition par
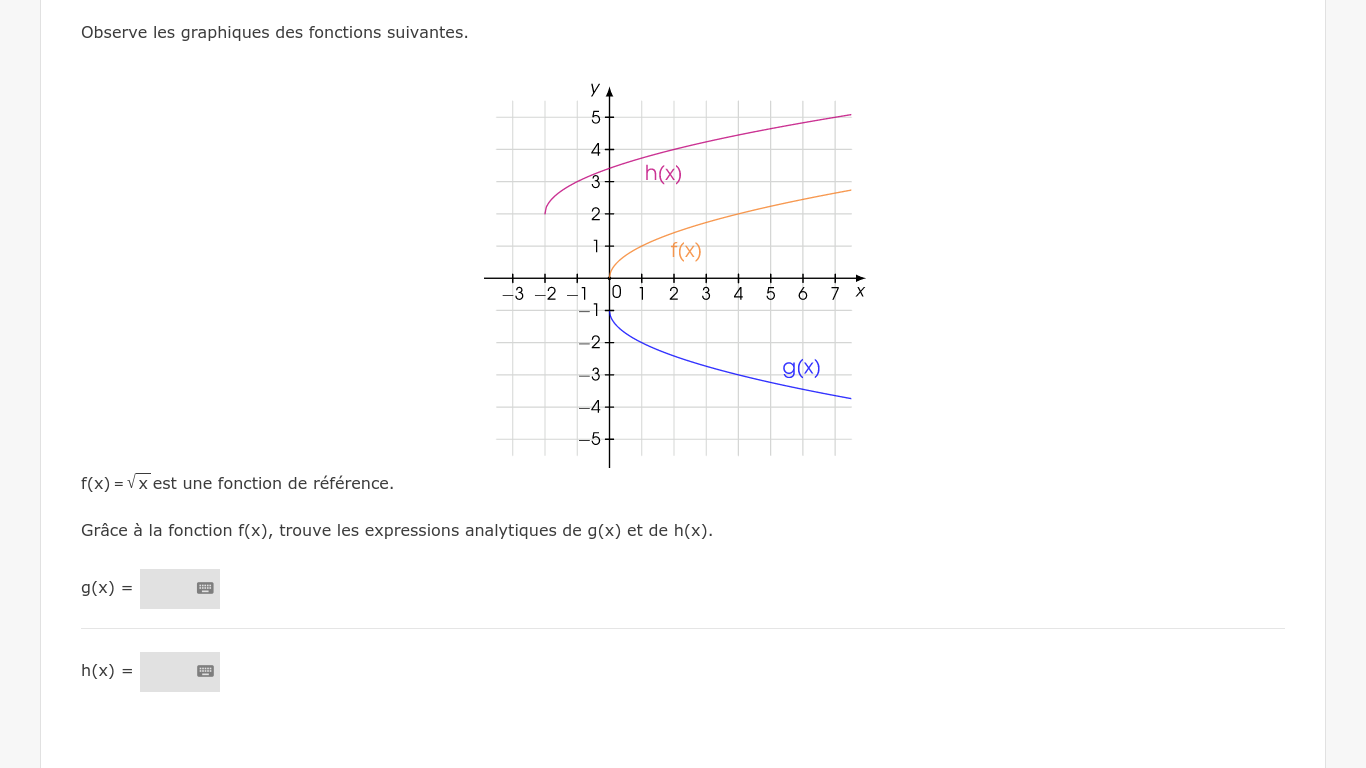
Capture d'écran effectué a partir du site "Oscar" dans le but de montrer un énoncé.@mtschoon voici mon énoncé, et il me faut complèter les partie grise dans les équations.
-
@Jérémie-Obsomer Bonjour,
Pour g(x)g(x)g(x), trace −f(x)-f(x)−f(x) et compare avec g(x)g(x)g(x), translation .....
Pour h(x)h(x)h(x), trace f(x)+2f(x)+2f(x)+2 et compare avec h(x)h(x)h(x).Indique tes éléments de réponse ou solution si tu souhaites une vérification.
-
mtschoon dernière édition par mtschoon

Bonjour,
Merci @Jérémie-Obsomer , d'avoir précisé ton énoncé.
Ce serait encore mieux de préciser le type de "fonctions racines" que tu cherches.
N'as -tu pas un titre explicite ? ou n'as tu pas un cours pour savoir ce qui a été étudié ?
Est-ce axa\sqrt xax ou ax\sqrt{ax}ax ou ax+b\sqrt{ax+b}ax+b ou ax+b\sqrt{ax}+bax+b ou x+b\sqrt x +bx+b ? ou ?Ce n'est pas très rigoureux de lire sur l'écran lorsque aucun point n'est indiqué.
Si tu peux indiquer plus, ce serait très bien..., sinon, ce sera de "l'à peu près..."
-
mtschoon dernière édition par mtschoon

J'essaie de "voir" les valeurs entières sur ton graphique.
Pour g, je crois lire :
g(0)=−1g(0)=-1g(0)=−1
g(1)=−2g(1)=-2g(1)=−2
g(4)=−3g(4)=-3g(4)=−3Vu l'ensemble de défintion de g, tu peux tenter g de la forme g(x)=ax+bg(x)=a\sqrt x+bg(x)=ax+b
Avec ces valeurs, tu dois trouver a=−1a=-1a=−1 et b=−1b=-1b=−1, d'où :
g(x)=−x−1g(x)=-\sqrt x -1g(x)=−x−1Il faut ensuite que tu t'assures que cette expression convient (approximativement) aux autres valeurs du graphique.
Pour h, je crois lire :
h(−2)=2h(-2)=2h(−2)=2
h(2)=4h(2)=4h(2)=4
h(7)=5h(7)=5h(7)=5Vu l'ensemble de définition de h , je te conseille de tenter h(x)=ax+2+bh(x)=a\sqrt{x+2}+bh(x)=ax+2+b
Je te laisse trouver a et b.
Bien sûr, ensuite, il faut t'assurer que l'expression trouvée convienne (approximativement) aux autres valeurs.Bonnes recherches et indique tes réponses si tu le souhaites.
-
Jérémie Obsomer dernière édition par
@mtschoon malheureusement non, je n'ai pas de cours explicite, c'est d'ailleurs la raison qui m'a poussé a tenté ma chance ici
-
Jérémie Obsomer dernière édition par
@mtschoon d'accord, mais, comment trouver a et b ?
-
mtschoon dernière édition par mtschoon

@Jérémie-Obsomer , bonjour,
Je te fais un calcul pour trouver a et b pour la fonction g proposée.
g(x)=ax+bg(x)=a\sqrt x+bg(x)=ax+b
Utilise les coordonnées de deux points ( vu qu'il y a deux inconnues a et b)
Le plus simple est d'utiliser g(0)=−1g(0)=-1g(0)=−1 et g(1)=−2g(1)=-2g(1)=−2g(0)=−1g(0)=-1g(0)=−1 <=> a0+b=−1a\sqrt 0+b=-1a0+b=−1 <=> b=−1b=-1b=−1
donc g(x)=ax−1g(x)=a\sqrt x-1g(x)=ax−1g(1)=−2g(1)=-2g(1)=−2 <=> a1−1=−2a\sqrt 1 -1=-2a1−1=−2 <=> a−1=−2a-1=-2a−1=−2 <=> a=1−2a=1-2a=1−2 <=> a=−1a=-1a=−1
donc g(x)=−x−1\boxed{g(x)=-\sqrt x-1}g(x)=−x−1Il te reste à vérifier que cette formule satisfait à g(4)=−3g(4)=-3g(4)=−3 et approximativement aux autres valeurs.
Lorsque tu auras compris, tu peux traiter h(x)=ax+2+bh(x)=a\sqrt{x+2}+bh(x)=ax+2+b de la même façon . Tu dois trouver a=1 et b=2 , c'est à dire h(x)=x+2+2\boxed{h(x)=\sqrt{x+2}+2}h(x)=x+2+2
Tu vérifes avec les autres points.
-
BBlack-Jack dernière édition par
Bonjour,
Visuellement :
Pour avoir la courbe représentant h(x), on doit "remonter" la courbe de f(x) de 2 unités et la faire glisser vers la gauche de 2 unités.
---> g(x) = f(x +2) + 2
g(x) = V(x+2) + 2 (avec V pour racine carrée)
On vérifie ensuite quelques points :
Par exemples :
g(-2) = V0 + 2 = 2, et on vérifie sur le graphe donné que le point de coordonnées (0;2) appartient bien à la courbe représentant h(x)
g(2) = V4 + 2 = 4, et on vérifie sur le graphe donné que le point de coordonnées (2;4) appartient bien à la courbe représentant h(x)
g(7) = V9 + 2 = 5, et on vérifie sur le graphe donné que le point de coordonnées (7;5) appartient bien à la courbe représentant h(x)C'est OK.