Recherche les points d'intersection des médiatrices et médianes d'un triangle, équations de droites.

Soit le triangle ABC défini par les coordonnées de ses sommets : A(0;0), B(2;4) et C(8;0).

Quelle est l'équation de chacune des médianes du triangle ABC ?

Calcule ensuite les coordonnées du point d'intersection des médianes du triangle ABC.

Bonjour, je suis de nouveau tombé en panne devant un énoncé de math, pourriez-vous s'il vous plait m'aidez à me remettre sur roue ?

@Jérémie-Obsomer , bonjour,
Une médiane est une droite passant par un sommet et le milieu du côté opposé.

Je t'explique pour la médiane issue de A
Soit I le milieu de [BC]
$xI=xB+xC2=2+82=5x_I=\dfrac{x_B+x_C}{2}=\dfrac{2+8}{2}=5$
$yI=yB+yC2=4+02=2y_I=\dfrac{y_B+y_C}{2}=\dfrac{4+0}{2}=2$

Donc $I (5; 2)$

Il te reste à trouver l'équation de la droite (AI)

Il y a plusieurs façons de la trouver.

Par exemple : équation de la forme $y = a x$ , vu que A est l'origine du repère.
La droite passe par I : $2 = 5 a$ <=> $a=25a=\dfrac{2}{5}$ d'où :
$y=25xy=\dfrac{2}{5}x$

Remarque : si la droite ne passait pas par l'origine, on aurait pris y=ax+b

Essaie de poursuivre et donne tes réponses si tu le souhaites.

Bonjour, j'ai essayé, mais je n'arrive pas,
En effet, j'ai appliqué les formules, et j'ai pu trouver tout les coordonnés des points situé a l'intersection des médianes et des côtés du triangle, je me retrouve donc avec
$A = (0; 0)$
$B = (2; 4)$
$C = (8; 0)$
$I = (5; 2)$ en sachant que $I$ est le milieu de la droite $B C$
$J = (1; 2)$ en sachant que $J$ est le milieu de la droite $A B$
$K = (4; 0)$ en sachant que $K$ est le milieu de la droite $A C$

ensuite, j'ai essayé de calculer les équations de types $f (x) = a x + b$ en me référant au "Cours de mathématiques de seconde > Déterminer l'équation d'une droite : l'essentiel" de MATHFORU. Qui m'indique que pour trouver l'équations, il faut simplement chercher à calculer les valeurs de $a$ et de $x$ dans l'équation réduite de la formule.
La valeur de $a$ - le coefficient directeur - est donnée par l'application de la formule :
$a=YB−YAXB−XAa=\dfrac{Y_B-Y_A}{X_B-X_A}$

Pour déterminer $b$ - l'ordonnée à l'origine - il suffit de résoudre l'équation d'inconnue $b$ :
$b=y_A-ax_a$

En appliquant donc ces formules pour la droite $A I$ :
$a=0−20−4=0,5a=\dfrac{0-2}{0-4}=0,5$ et non pas $a=25a=\dfrac{2}{5}$ comme tu l'as trouvée. Mais, je ne trouve pas mon erreur.
Pourriez-vous s'il vous plait m'aidez ?

@Jérémie-Obsomer Bonjour,

Pour le coefficient directeur de la droite $(A I)$ , utilise les coordonnées des points A et I.

$a=YI−YAXI−XA=2−05−0=....a=\dfrac{Y_I-Y_A}{X_I-X_A}=\dfrac{2-0}{5-0}=....$

Ah, bête erreur, merci
je me retrouve donc bien avec $a=25a=\dfrac{2}{5}$

Je me retrouve donc avec
$f(x)=25xf(x)=\frac{2}{5}x$ pour la droite ( $A I$ )
$f(x)=−16x+136f(x)=-\frac{1}{6}x+\frac{13}{6}$ pour la droite ( $C J$ )
$f (x) = - 2 x + 8$ pour la droite ( $B K$ )
est-ce correct ?
Merci beaucoup

@Jérémie-Obsomer a dit dans Recherche les points d'intersection des médiatrices et médianes d'un triangle. :

Je me retrouve donc avec
$f(x)=25xf(x)=\frac{2}{5}x$ pour la droite ( $A I$ )
$f(x)=−16x+136f(x)=-\frac{1}{6}x+\frac{13}{6}$ pour la droite ( $C J$ )
$f (x) = - 2 x + 8$ pour la droite ( $B K$ )
est-ce correct ?
Merci beaucoup

Bonjour,

Equation de (CJ) fausse.

Il n'est pas non plus judicieux de donner le même nom (f(x)) pour les représentations de 3 droites différentes.

@Black-Jack
Ce serait $f(CJ)=16x+116f(CJ)=\frac{1}{6}x+\frac{11}{6}$ ?

@Jérémie-Obsomer

Indique tes calculs,
Le coefficient directeur de la droite $(C J)$ : $\dfrac{2-0}{1-8}=....$

Bonsoir,

@Jérémie-Obsomer a dit dans Recherche les points d'intersection des médiatrices et médianes d'un triangle. :

Soit le triangle ABC défini par les coordonnées de ses sommets : A(0;0), B(2;4) et C(8;0).
Quelle est l'équation de chacune des médianes du triangle ABC
Calcule ensuite les coordonnées du point d'intersection des médianes du triangle ABC.

@Jérémie-Obsomer , pour plus de clarté et pour pouvoir vérifier les résultats, je joins un schéma.

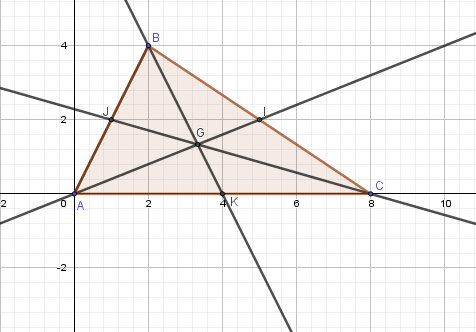
médianes.jpg

@Jérémie-Obsomer ,

Quelques remarques,

Pour (AI) ,en appelant f la fonction affine, tu peux écrire $f(x)=25xf(x)=\dfrac{2}{5}x$
Tu peux aussi écrire que l'équation réduite de la droite (AI) est $y=25xy=\dfrac{2}{5}x$

Par contre, comme cela a déjà été indiqué, pour (CJ), il n'est pas correct d'utiliser f vu qu'il ne s'agit pas de la même fonction affine que pour (AI).
Tu peux écrire, par exemple, g(x)=....( à recompter vu que ton "a" est inexact et le b aussi, en conséquence )

Pour (BK) , c'est bon.
Tu peux écrire , par exemple, en appelant h la fonction affine $h (x) = - 2 x + 8$
ou bien, tu peux dire que l'équation réduite de (BK) est $y = - 2 x + 8$

Pour vérification, si tu le souhaites, tu donnes donc ta réponse pour (CJ)

Eh bien, pour $g (x) = a x + b$ , j'ai fais comme suit :
$a=yC−yJxC−xJ=0−28−1=−27=−27a=\dfrac{y_C-y_J}{x_C-x_J}=\dfrac{0-2}{8-1}=\dfrac{-2}{7}=-\dfrac{2}{7}$
$b=g(x)−ax=yJ−(−27)xJ=2+27∗1=167b=g(x)-ax=y_J-(-\dfrac{2}{7})x_J=2+\dfrac{2}{7}*1=\dfrac{16}{7}$
je me retouve donc avec:
$g(x)=−27x+167g(x)=-\dfrac{2}{7}x+\dfrac{16}{7}$
Est-ce juste ?
Merci d'avance.

@Jérémie-Obsomer ,

Oui, c'est juste pour (CI). Bravo !

Il te reste à trouver les coordonnées de G , centre de gravité du triangle, intersection des 3 médianes.

Bien sur, pour les calculs, tu peux te contenter de trouver les coordonnées du point d'intersection de deux médianes ( prends les équations qui te paraissent les plus simples, par exemple $y=25xy=\frac{2}{5}x$ et $y = - 2 x + 8$

Ensuite, tu peux vérifier que le point G trouvé est bien sur la 3ème médiane.

Sauf erreur , tu dois trouver $G(103,43)G(\dfrac{10}{3}, \dfrac{4}{3})$

Reposte si tu as des difficultés dans les calculs.

@mtschoon
et bien, a vrai dire, je ne sait pas comment faire

@Jérémie-Obsomer

Pour trouver l'abscisse du point $G$ , tu résous l'équation : $25x=−2x+8\dfrac{2}{5}x= -2x+8$ .
Pour l'ordonnée du point $G$ , tu remplaces $x$ par la valeur trouvée dans $y=25xy=\dfrac{2}{5}x$ .

Bonjour,

@Jérémie-Obsomer

Tu as un système de deux équations à résoudre
${y=25xy=−2x+8\begin{cases}y=\dfrac{2}{5}x\cr y=-2x+8\end{cases}$

Tu as déjà la piste.

Bien sûr, reposte si tu n'y arrives pas.

Pour maîtriser le principe et t'entraîner, tu peux regarder le lien ici :
https://www.mathforu.com/troisieme/resolution-de-systemes-d-equations/

Voila comment j'ai fait:
-tout d'abord, j'ai isolé le $x$ dans la première expression:
$y=25xy=\dfrac{2}{5}x$ ce qui me donne, $x=52yx=\dfrac{5}{2}y$
-puis, j'ai remplacé le $x$ dans la deuxième expression:
$y = - 2 x + 8$ ce qui me donne, $y=−2(52y)+8y=-2(\dfrac{5}{2}y)+8$
-ensuite, j'ai résolu l'équation:
$y=−2(52y)+8y=-2(\dfrac{5}{2}y)+8$
$−8=y−(−2)(52y)-8=y-(-2)(\dfrac{5}{2}y)$
$- 8 = y - (- 5) y = y + 5 y$
$- 8 = 6 y$
$y=−86y=-\dfrac{8}{6}$
C'est faux, je le sais, mais où ?
Tandis que pour l'ordonnée, je n’ai pas compris comment il fallait que je fasse

@Jérémie-Obsomer ,

Tout d'abord, c'est très bien d'utiliser le Latex car c'est plus clair.

Je regarde tes calculs.

C'est juste jusqu'à $y=−2(52y)+8y=-2(\dfrac{5}{2}y)+8$

Ensuite il y a des erreurs de signe en transposant

Tu aurais dû écrire : $−8=−y−2(52y)-8=-y-2(\dfrac{5}{2}y)$
c'est à dire : $- 8 = - y - 5 y$
c'est à dire : $- 8 = - 6 y$
c'est à dire : $−8−6=y\dfrac{-8}{-6}=y$
c'est à dire : $86=y\dfrac{8}{6}=y$
c'est à dire : $43=y\boxed{\dfrac{4}{3}=y}$
Ensuite, connaissant y, tu déduis x avec une des deux équations
(et tu peux vérifier en prenant l'autre)
Par exemple :
$x=52(43)x=\dfrac{5}{2}(\dfrac{4}{3})$
c'est à dire : $x=206x=\dfrac{20}{6}$
c'est à dire : $x=103\boxed{x=\dfrac{10}{3}}$

J'ai essayé de détailler le mieux possible, mais demande si quelque chose ne te va pas.

@Jérémie-Obsomer ,

Je te mets l'autre méthode, en commençant par calculer x.

${y=25xy=−2x+8\begin{cases}y=\dfrac{2}{5}x\cr y=-2x+8\end{cases}$

Tu remplaces y par $25x\dfrac{2}{5}x$ dans la seconde équation :

$25x=−2x+8\dfrac{2}{5}x=-2x+8$

En transposant : $25x+2x=8\dfrac{2}{5}x+2x=8$
c'est à dire : $2x+10x5=8\dfrac{2x+10x}{5}=8$
c'est à dire : $12x5=8\dfrac{12x}{5}=8$
c'est à dire : $12 x = 40$
c'est à dire : $x=4012x=\dfrac{40}{12}$
c'est à dire ; $x=103\boxed{x=\dfrac{10}{3}}$

Ensuite, connaissant x, tu déduis y avec une des deux équations
(et tu peux vérifier en prenant l'autre)
Par exemple :
$y=25(103)y=\dfrac{2}{5}(\dfrac{10}{3})$
c'est à dire : $y=2(23)y=2(\dfrac{2}{3})$
c'est à dire : $y=43\boxed{y=\dfrac{4}{3}}$

Tu as le choix.

Entraîne toi à faire les deux méthodes : commencer par calculer y puis en déduire x, ou bien commencer par calculer x puis en déduire y.

@mtschoon j'ai essayé une autre méthode pour calculer l'abscisse:
je suis parti de $y=−2(52)y+8y=-2(\dfrac{5}{2})y+8$
j'ai donc fait:
$y=−2(52)y+8y=-2(\dfrac{5}{2})y+8$
$y = - 5 y + 8$
$0 = - 6 y + 8$
$0=−y+860=-y+\dfrac{8}{6}$
$y=86=43y=\dfrac{8}{6}=\dfrac{4}{3}$

@Jérémie-Obsomer ,

C'est parfait !

@mtschoon Merci,
j'ai donc comtinué mes exercices, et je me retrouve face a ce problème,
"Détermine les coordonnées du point d'intersection entre la droite d $_1$ et la droite d $_2$ dont on connaît les équations."
d $1≡x=3_1\equiv x=3$
d $2≡2y−3x−5=0_2\equiv 2y - 3x - 5=0$
C'est bien des équations de droite linéaire ça?

@Jérémie-Obsomer a dit dans Recherche les points d'intersection des médiatrices et médianes d'un triangle. :

@mtschoon Merci,
j'ai donc comtinué mes exercices, et je me retrouve face a ce problème,
"Détermine les coordonnées du point d'intersection entre la droite d $_1$ et la droite d $_2$ dont on connaît les équations."
d $1≡x=3_1\equiv x=3$
d $2≡2y−3x−5=0_2\equiv 2y - 3x - 5=0$
C'est bien des équations de droite linéaire ça?

Bonjour,

Ce sont bien des équations de droites.
Mais ne pas confondre "fonction linéaire" et "Equation d'une droite."

Wiki donne :
Une fonction linéaire est une fonction simple des mathématiques élémentaires, qui traduit la proportionnalité et qui se traduit en langage mathématique par les termes f(x) = ax.

Donc les droites passant par l'origine du repère sont représentées par des fonctions linéaires ...

La droite d'équation x = 3 ... est celle de la droite parallèle à l'axe des ordonnées passant par le point de coordonnées (3 ; 0)

2y−3x−5=0 est l'équation d'une droite de coefficient directeur m = 3/2 et passant par exemple par le point de coordonnées (0 ; 5/2)

Les coordonnes du point d'intersection de d1 et d2, se trouvent en résolvant le système :

x = 3
2y-3x-5 = 0

Voila, il n'y a plus qu'à ...

@Jérémie-Obsomer ,
La droite $d_1)$ est parallèle à l'axe des ordonnées.
La droite $d_2)$ est la représentation d'une fonction affine (de la forme $y=ax+b=32x+52y=ax+b=\dfrac{3}{2}x+\dfrac{5}{2}$ mais non linéaire vu qu'elle ne passe pas par l'origine du repère (b n'est pas nul)

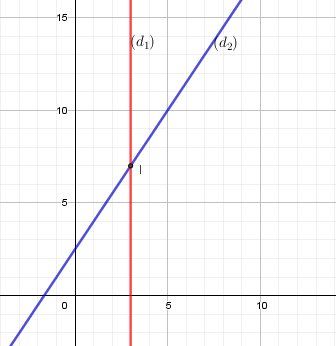
En remplaçant x par 3 dans la seconde équation, tu trouves y.
Tu peux donner ta réponse pour vérification si tu le souhaites.

Remarque : effectivement, tu es toujours sur le thème des équations de droites, mais le titre que tu as donné au topic "Recherche les points d'intersection des médiatrices et médianes d'un triangle", n'est plus adapté...

Vu que tu n'as pas changé de discussion (ce qui aurait été mieux) , modifie le titre, pour mettre un titre plus adapté, du genre "médianes d'un triangle et équations de droites".

Rappel : une discussion= un exercice.
Ne l'oublie pas une autre fois.

Donc, on a:
$x = 3$
$0 = 2 y - 3 x - 5$
et on fait:
$0 = 2 y - 3 * 3 - 5$
$0 = 2 y - 9 - 5$
$0 = 2 y - 14$
$0 = y - 7$
$y = 7$
on a donc comme coordonées:
$(3; 7)$

@Jérémie-Obsomer ,

C'est tout à fait ça.

Sur le graphique , tu peux vérifier que $(3, 7)$ sont les coordonnées du point I intersection des droites $d_1)$ et $d_2)$

N'oublie pas de changer le titre de ce topic et pour un autre exercice, ouvre une autre discussion

@mtschoon je peut pas changer le titre

@Jérémie-Obsomer ,

Tant pis pour le titre...

Peut-être que la modération le fera.

Bonne soirée !

Bonjour,

Merci à la modération d'avoir ajouter "équations de droites" dans le titre.

Bonjour,

Je vois que la recherche du point d'intersection des médiatrices n'a pas été traité.

Pour consultation éventuelle, j'indique quelques pistes pour répondre à cette question.
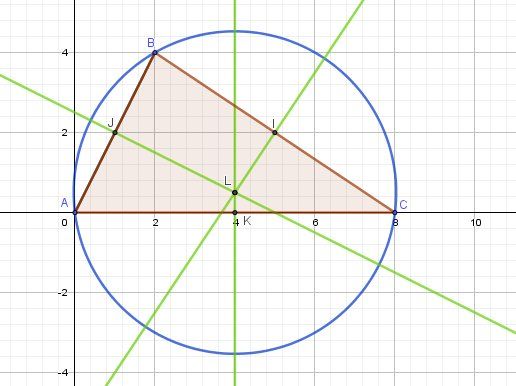
médiatrices.jpg

Repère necessairement orthonormé.
Les coordonnées de I,J,K ont déjà été calculés.
$I (5, 2); J (1, 2); K (4, 0)$

Equation de la médiatrice passant par K : $x=4\boxed{x=4}$ (car parallèle à l'axe des ordonnées)

Recherche de la médiatrice passant par I
Soit a le coefficient directeur de (BC)
$a=yC−yBxC−xBa=\dfrac{y_C-y_B}{x_C-x_B}$
Après calcul $a=−23a=-\dfrac{2}{3}$
Soit a' le coefficient directeur de la médiatrice passant par I
Par théorème $a a^{'} = - 1$ (car droites perpendiculaires)
donc $a′=−1a=32a'=\dfrac{-1}{a}=\dfrac{3}{2}$
L'équation cherchée peut s'écrire $y=32x+by=\dfrac{3}{2}x+b$
En utilisant les coordonnées de I : $2=32(5)+b2=\dfrac{3}{2}(5)+b$
d'où $b=−112b=-\dfrac{11}{2}$
Equation de la médiatrice passant par I : $y=32x−112\boxed{y=\dfrac{3}{2}x-\dfrac{11}{2}}$
Soit L le point d'inrersection des médiatrices du triangle ABC
Les coordonnées de L sont solutions du système :
${x=4y=32x−112\begin{cases} x=4\cr y=\dfrac{3}{2}x-\dfrac{11}{2}\end{cases}$
Après calcul : L a pour coordonnées $(4,12)\boxed{(4,\dfrac{1}{2})}$

Remarque : Pour vérification, on peut chercher l'équation de la 3ème médiatrice et s'assurer qu'elle passe par L

Complément non demandé : L est le centre du cercle circonscrit au triangle ABC.
Soit R le rayon de ce cercle
$R=LA=(xA−xL)2+(yA−yL)2=654R=LA=\sqrt{(x_A-x_L)^2+(y_A-y_L)^2}=\sqrt{\dfrac{65}{4}}$
L'équation ce cercle est donc : $x-x_L)^2+(y-y_L)^2=R^2$ , c'est à dire :
$(x−4)2+(y−12)2=654\boxed{(x-4)^2+(y-\dfrac{1}{2})^2=\dfrac{65}{4}}$
Si l'on préfère les nombres décimaux :
$(x−4)2+(y−0.5)2=16.25\boxed{(x-4)^2+(y-0.5)^2=16.25}$

Bonne lecture éventuelle.