Détermine l'équation d'une droite passant par un point et dont la direction est donnée

Détermine une équation cartésienne de la droite $d$ passant par le point $A (x_A;y_A)$ et de vecteur directeur $u (x_u;y_u)$ pour mon premier énoncé

Bonjour,
Est-ce que quelqu'un pourrait m'aider à résoudre ce problème ?
Merci d'avance a vous tous

@Jérémie-Obsomer Bonjour, (Marque de politesse à ne pas oublier !!)

Utilise la propriété : Si une droite a pour équation cartésienne $a x + b y + c = 0$ , alors le vecteur de coordonnées $a)(-b\ ;\ a)$ est un vecteur directeur de cette droite.

Bonjour @Noemi,
Mais pourquoi donne ton les coordonnées d'un point a un vecteur censé être un segment de droite ?

@Jérémie-Obsomer

Les coordonnées d'un point permettent de déterminer la valeur de $c$ .
Fais un exemple.

Bonjour,

@Jérémie-Obsomer , n'oublie pas la politesse quand tu commences une discussion...

Si besoin, je te mets un lien vers un exemple numérique qui correspond exactement à ton énoncé.
https://www.youtube.com/watch?v=4NXgsUSKrrk

Lorsque tu l'as compris, fais de même avec les notations de ton énoncé (sans valeurs numériques) et donne tes réponses si tu le souhaites.

@Jérémie-Obsomer , bonjour,

Comme je vais être absente quelques jours (vacances obligent!), j'explicite la piste possible que je t'ai indiquée pour être sûre que tu l'as bien assimilée.

M est un point quelconque de (d) de coordonnées (x,y)

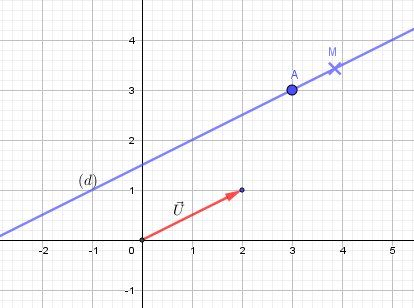
Les coordonéées du verteur $AM→\overrightarrow{AM}$ sont : $x−xAy−yA\begin{matrix}x-x_A\cr y-y_A\end{matrix}$

Les coordonnées du vecteur $U→\overrightarrow{U}$ (non vecteur nul) sont : $xU→yU→\begin{matrix}x_{\overrightarrow U} \cr y_{\overrightarrow U}\end{matrix}$

$AM→\overrightarrow{AM}$ et $U→\overrightarrow{U}$ sont colinéaires.

D'après la propriété caractéristique des vecteurs colinéaires relative aux produits en croix :
$(x−xA)(yU→)=(y−yA)(xU→)\boxed{(x-x_A)(y_{\overrightarrow U})=(y-y_A)(x_{\overrightarrow U})}$

Tu pourrais mettre cette équation sous la forme y=ax+b (avec certaines conditions), mais vu que c'est une équation cartésienne qui est demandée, tu mets cette équation sous la forme $a x + b y + c = 0$ avec $(a,b)≠(0,0)(a,b)\ne (0,0)$

Pour cela, tu transposes le tout dans le membre de gauche :
$(x−xA)(yU→)−(y−yA)(xU→)=0(x-x_A)(y_{\overrightarrow U})-(y-y_A)(x_{\overrightarrow U})=0$

Tu développes et tu regroupes comme nécessaire .

Sauf erreur, tu dois trouver :
$(yU→)x+(−xU→)y+(−xAyU→+yAxU→)=0\boxed{(y_{\overrightarrow U})x+(-x_{\overrightarrow U})y+(-x_Ay_{\overrightarrow U}+y_Ax_{\overrightarrow U})=0}$

Remarque : si tu veux vérifier avec les valeurs numériques du lien que je t'ai donné, tu prends $x_A=-3$ , $y_A=4$ , $xU→=−1x_{\overrightarrow U}=-1$ et $yU→=2y_{\overrightarrow U}=2$
Tu trouveras pour équation cartésienne : $2 x + y + 2 = 0$ , c'est à dire $y = - 2 x - 2$ qui est l'équation réduite trouvée dans le lien.

Bon travail.

@Jérémie-Obsomer ,

Pour consultation éventuelle.

Tu as ici un cours de Seconde (français) sur les vecteurs.
La propriété utilisée dans cet exercice est la propriété 5 du paragraphe III (Colinéarité)

https://www.mathforu.com/seconde/les-vecteurs-en-2nd/

Bonne lecture.

Bonjour,
Est-ce que je ne peux pas, tout simplement, prendre le point $A (- 1; 2)$ et avec le vecteur $u (3; - 7)$ , trouver un point $C(x_c;y_c)$ appartenant à la droite en faisant:
$x_A+x_u=x_c$ soit $- 1 + 3 = 2$ et $y_A+y_u=y_c$ soit $2 + (- 7) = - 5$
Et ensuit calculer l'équation de la droite a partir des points $A$ et $C$ ?
Ce qui me donnerais:
$d1≡y=ax+bd_1 \equiv y=ax+b$
$a=2−(−5)(−1)−2=7(−3)=−73a=\dfrac{2-(-5)}{(-1)-2}=\dfrac{7}{(-3)}=-\dfrac{7}{3}$
et $b=ya−axa=2−(−73)∗(−5)=−293b=y_a-ax_a=2-(-\dfrac{7}{3})*(-5)=-\dfrac{29}{3}$
Ce qui me donne: $d1≡f(x)=−73x+(−293)d_1\equiv f(x)=-\dfrac{7}{3}x+(-\dfrac{29}{3})$
Est ce juste ?
Merci d'avance

@Jérémie-Obsomer Bonjour,

C'est faux, vérifie les calculs et/ou utilise les indications qui t'ont été données.

@Jérémie-Obsomer a dit dans Détermine l'équation d'une droite passant par un point et dont la direction est donnée :

Bonjour,
Est-ce que je ne peux pas, tout simplement, prendre le point $A (- 1; 2)$ et avec le vecteur $u (3; - 7)$ , trouver un point $C(x_c;y_c)$ appartenant à la droite en faisant:
$x_A+x_u=x_c$ soit $- 1 + 3 = 2$ et $y_A+y_u=y_c$ soit $2 + (- 7) = - 5$
Et ensuit calculer l'équation de la droite a partir des points $A$ et $C$ ?
Ce qui me donnerais:
$d1≡y=ax+bd_1 \equiv y=ax+b$
$a=2−(−5)(−1)−2=7(−3)=−73a=\dfrac{2-(-5)}{(-1)-2}=\dfrac{7}{(-3)}=-\dfrac{7}{3}$
et $b=ya−axa=2−(−73)∗(−5)=−293b=y_a-ax_a=2-(-\dfrac{7}{3})*(-5)=-\dfrac{29}{3}$
Ce qui me donne: $d1≡f(x)=−73x+(−293)d_1\equiv f(x)=-\dfrac{7}{3}x+(-\dfrac{29}{3})$
Est ce juste ?
Merci d'avance

Bonjour,

On peut aussi y arriver comme cela ... mais la fin est fausse.

Pour le calcul de b, c'est le point C qu'il faut utiliser ... tu l'as fait bien bien que tu as écrit x_a et y_a (au lieu de x_c et y_c)
MAIS, dans les calculs tu as inversé les valeurs de x_c et y_c

OK pour le début ...

Mais ensuite : b = y_c - a * x_c
b = -5 - (-7/3) * 2
b = -5 + 14/3
b = -1/3

d1 : y = -(7/3).x - (1/3)

@Jérémie-Obsomer

Pour le calcul de $b$ , l'erreur vient des coordonnées du point $A$ :
$b=y_a-ax_a$
$b=2−(−73)×(−1)=2−(73)=−13b=2-(-\dfrac{7}{3})\times(-1)=2-(\dfrac{7}{3})=-\dfrac{1}{3}$

soit pour l'équation de $d_1$ :
$y=−73x−13y=-\dfrac{7}{3}x-\dfrac{1}{3}$
ou
$7 x + 3 y + 1 = 0$

@Noemi @Black-Jack Bonjour, et merci beaucoup pour vos réponses,
Mais, un point important dans l'énoncé m'avait échappé, on demande une équation cartésienne, soit : $a x + b y + c = 0$
Donc, j'ai appliqué une autre méthode : j'ai utilisé la propriété qui dit que les coordonnées du vecteur $u$ peuvent être utilisé comme ceci : $(−b;a)(x;y)\implies(-b;a)$ .
Cette propriété est-elle toujours valable ?
Ensuite, il me suffit d'utiliser les coordonnées du point $A$ dans l’équation pour trouver $c$
ce qui me donne :
$A (3; 1)$ et $U (5; 3)$
donc :
$3x+(−5)y+c=0ax+by+c=0\implies3x+(-5)y+c=0$
ensuite, pour trouver $c$ :
$a x + b y = - c$
$3 * 3 + (- 5) * 1 = - c$
$9 - 5 = - c$
$4 = - c$
$- 4 = c$
je me retrouve donc avec l'équation cartésienne :
$3 x + (- 5) y + (- 4) = 0$
et si je veut la passer en équation réduite de type $y = m x + p$ , j'ai fait:
$3 x + (- 5) y + (- 4) = 0$
$3 x + (- 5) y = - (- 4) = 4$
$- 5 y = 4 - 3 x$
$y=4−5−3−5xy=\dfrac{4}{-5}-\dfrac{3}{-5}x$
$y=−35x+(−45)y=-\dfrac{3}{5}x+(-\dfrac{4}{5})$
Ai je fais des erreurs ?
Merci encore de votre aide, elle m'a été très utile.

@Jérémie-Obsomer

La méthode est correcte, elle correspond à la piste que j'ai indiquée dans mon premier post.
Pour le calcul, tu utilises comme vecteur directeur $u→(5;3)\overrightarrow{u}(5;3)$ or dans l'énoncé c'est : $u→(3;−7)\overrightarrow{u}(3;-7)$ .
Donc tu ne peux pas retrouver l'équation indiquée, soit $7 x + 3 y + 1 = 0$ .
Il est demandé l'équation cartésienne, donc tu peux conclure avec $7 x + 3 y + 1 = 0$ .

@Noemi Bonjour,
Oui, en effet, ce ne sont pas les coordonnées de mon énoncé, je me suis entrainé avec des coordonnées différentes, et si je reprends mon énoncé, j'ai, comme coordonnée :
$A (- 1; 2)$ et $u (3; - 7)$
ensuite, j'applique la méthode,
$a x + b y + c = 0$
$(- 7) x + (- 3) y + c = 0$
$(- 7) * (- 1) + (- 3) * 2 + c = 0$
$7 + (- 6) = - c$
$1 = - c$
$- 1 = c$
j'arrive donc a :
$\implies (-7)x-3y-1=0$
Pourquoi, moi j'arrive avec que des nombres négatifs ?

@Jérémie-Obsomer

C'est juste aussi avec des nombres négatifs.
Multiplie par $(- 1)$ l'équation et tu trouves $7 x + 3 y + 1 = 0$ .