Continuité et dérivation

[ABCD EFGH]

Bonjour j'ai une question :
Soit f une fonction définie par
● f(x)=cos((pi/2)x) / x - 1 ; x différent de 1
● f(1)=a
Alors la question est trouver la valeur de a pour que f soit continue en 1 .
Ce que j'ai fait :
f est continue en 1 si lim de f(x) quand x tend vers 1 égale f(1).
Le calcule de cette limite est un peu compliqué, donc ce que j'ai fait c'est de la calculer à l'aide de la dérivée :
Soit g(x) = cos((pi/2)x) ; g(1)=0
Donc lim de f(x) quand x tend vers 1 = lim de g(x) - g(1) / x - 1 quand x tend vers 1
Et comme g est dérivable sur R donc elle est dérivable en 1 et par la suite lim de f(x) quand x tend vers 1 = g'(1) = f(1) = a
Et comme g'(x) = - pi/2 sin((pi/2)x)
Donc g'(1) = - pi/2
Par conséquent a = - pi/2
Mon raisonnement est-il suffisant et sensé , et merci d'avance

[Black-Jack]

Bonjour,

cos(Pi/2).x) = - sin(Pi/2).x - Pi/2)

cos((pi/2)x) / (x - 1) = - sin((Pi/2)*(x-1))/(x-1)

cos((pi/2)x) / (x - 1) = -(Pi/2) * sin((Pi/2)*(x-1))/(Pi/2).(x-1))

Et en posant (Pi/2)*(x-1) = y ---> cos((pi/2)x) / (x - 1) = -(Pi/2) * sin(y)/y

si x -->1, on a y --> 0 et donc

lim(x-->1) f(x) = lim(y-->0) [-(Pi/2) * sin(y)/y] = -Pi/2

[Noemi]

@ABCD-EFGH Bonjour,

Ton raisonnement est correct.

[mtschoon]

Bonjour,

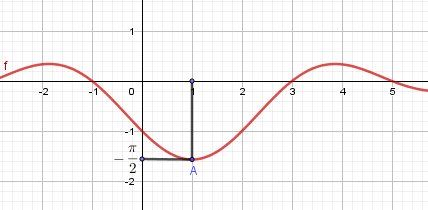
Illustration graphique.

Le point $A(1,-\frac{\pi }{2})$ permet le prolongement par continuité de de la fonction f en $x=1$.