Exercice sur la recurrence

Bonjour,

Je ne comprends pas comment (n(n+1)(n+2))/2 + (n+1)(n+2) devient (n+1)(n+2)(n/3+1) et aussi pourquoi la partie (n+1)(n+2) du résultat à la fin est sur 3,

j'ai compris pour le n+3 mais pour (n+1)(n+2)... Expliquez moi svp

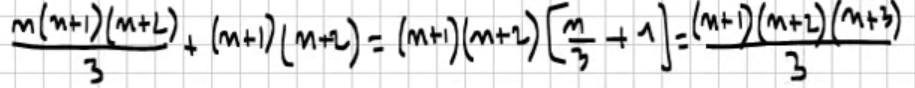
@Isra-K Bonjour,

La première partie est une factorisation :
$n(n+1)(n+2)3+(n+1)(n+2)=(n+1)(n+2)×n3+(n+1)(n+2)×1\dfrac{n(n+1)(n+2)}{3}+(n+1)(n+2)= (n+1)(n+2)\times\dfrac{n}{3}+(n+1)(n+2)\times 1$
soit $(n+1)(n+2)(n3+1)(n+1)(n+2)(\dfrac{n}{3}+1)$

Puis si on réduit $(n3+1)(\dfrac{n}{3}+1)$ au même dénominateur :

$(n3+1)=(n3+33)=(n+33)(\dfrac{n}{3}+1)= (\dfrac{n}{3}+\dfrac{3}{3}) = (\dfrac{n+3}{3})$