dérivation , exercices
-
Ppouvens dernière édition par
bonjour vous pouvez m'aider svp
je suis bloquéeExercice 3
Étudier les variations de la fonction f définie sur R par f(x)= (1-x)e²x +1
j ai commencé par dire que la fonction est dérivable sur R car c'est le produit d'une fonction polynome et d'une fonction exponentielle
et que c est de la forme uxv
avec u(x)=1-x et v(x)= e²x+1
-
@pouvens bonsoir,
u(x)=1−xu(x) = 1-xu(x)=1−x, u′(x)=−1u'(x)= -1u′(x)=−1
Si v(x)=e2xv(x)= e^{2x}v(x)=e2x, alors v′(x)=2e2xv'(x)= 2e^{2x}v′(x)=2e2x
Je te laisse poursuivre
-
Ppouvens dernière édition par
f'(x)= -1(e²x+1) + 2e²x ( 1-x)
= -e²x-1 + 2e²x + 2e²x²
-
Attention,
v(x)v(x)v(x) n'est pas égal à e2x+1e^{2x}+1e2x+1 puisqu'il n'y a pas de parenthèse.Est-ce e2x+1e^{2x+1}e2x+1 ?
-
Ppouvens dernière édition par
non , le 1 n'est pas en exposant
-
Donc si f(x)=(1−x)e2x+1f(x)= (1-x)e^{2x}+1f(x)=(1−x)e2x+1
tu poses
u(x)=(1−x)u(x)= (1-x)u(x)=(1−x) et v(x)=e2xv(x)= e^{2x}v(x)=e2x
puis
u′(x)=−1u'(x)= -1u′(x)=−1 et v′(x)=2e2xv'(x)= 2e^{2x}v′(x)=2e2x
soit
f′(x)=−1×e2x+(1−x)×2e2xf'(x)= -1\times e^{2x}+(1-x)\times 2e^{2x}f′(x)=−1×e2x+(1−x)×2e2x
A simplifier
-
Ppouvens dernière édition par
et le +1???
f'(x)= e²x +2e²x-2e²x²
-
La dérivée d'une constante est nulle.
Attention aux signes
f′(x)=e2x(−1+2−2x)f'(x)= e^{2x}(-1+2-2x)f′(x)=e2x(−1+2−2x)
soit f′(x)=(1−2x)e2xf'(x)=(1-2x)e^{2x}f′(x)=(1−2x)e2xEtudie le signe de cette dérivée.
-
Ppouvens dernière édition par
@Noemi
1-2x supérieur ou égal à 0
X supérieur ou égal à 1/2
Dc de moins l infini à 1/2 f '(x) est négative et de 1/2 à plus l infini elle est positiveDc f est décroissante puis croissante
-
@pouvens
Non1−2x≥01-2x\geq01−2x≥0 ; −2x≥−1-2x \geq -1−2x≥−1, soit x≤12x \leq \dfrac{1}{2}x≤21
-
Ppouvens dernière édition par
@Noemi
Ah oui c'est vrai
Merci
Du coup la fonction est croissante puis décroissante
-
Oui, ce sont les bonnes variations.
-
Ppouvens dernière édition par
@Noemi
Et pour e2x
-
e2xe^{2x}e2x est strictement positif pour tout xxx.
-
mtschoon dernière édition par

Bonjour,
@pouvens , je regarde ton travail.
Tu as commencer par indiquer :
"La fonction est dérivable sur R car c'est le produit d'une fonction polynome et d'une fonction exponentielle"ça ne va pas à cause du "+1"
f(x)=(1−x)e2x+1f(x)=(1-x)e^{2x}+1f(x)=(1−x)e2x+1
Tu peux, par exemple, poser : f(x)=g(x)+h(x)f(x)=g(x)+h(x)f(x)=g(x)+h(x) avec
g(x)=(1−x)e2xg(x)=(1-x)e^{2x}g(x)=(1−x)e2x et h(x)=1h(x)=1h(x)=1
ggg est dérivable comme produit de deux fonctions dérivables (fonction polynôme et fonction exponentielle)
hhh est dérivable comme fonction constante (sa dérivée vaut 0)Donc fff est dérivable comme somme de deux fonctions dérivables ggg et hhh
-
mtschoon dernière édition par

@pouvens ,
Si tu veux vérifier les variations de f que tu as trouvées, sur la calculette, tu peux faire représenter f.
Voici une illustration :
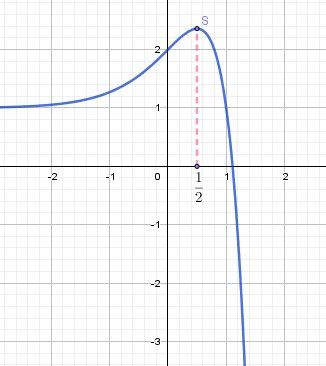
-
Ppouvens dernière édition par
@mtschoon d accord merci beaucoup
-
mtschoon dernière édition par

De rien @pouvens et bon travail.