probabilite denombrement
-
Lloicstephan dernière édition par
bonsoir a tous ! heureux de vous retrouver
Lors d ' un examen, le professeur propose un QCM composé de 4 questions. Pour chaque question, il y a 5 ré-
ponses et l'étudiant doit choisir l' une d'entre elles. On
admet que pour chaque question, une seule réponse est
exacte.- Déterminer le nombre de grilles-réponses possibles.
- Quelle est la probabilité qu' un étudiant réponde au
hasard correctement à au moins 2 questions et obtienne ainsi au moins la moyenne sur cet exercice ?
perso pour mla question 1
je denombre 5*4 grille de reponse
pour la question 2
je trouve P(X superieur ou egal a 2)=9/5
-
@loicstephan Bonsoir,
je suppose que pour la première question tu as voulu écrire 545^454.
Pour la deuxième question calcule la probabilité de l'événement contraire.
-
Lloicstephan dernière édition par
la premiere question question je ne la comprend pas bien
pour la deuxieme question la proba de l'evennement contraire donne 1−151-\frac{1}{5}1−51 ce qui donne 4/5
-
Pour chaque question, 5 réponses sont possibles donc le nombre de grilles réponses possibles est
5×5×5×5=545\times 5\times 5\times 5 =5^45×5×5×5=54Pour la question 2, quelle est la probabilité d'avoir :
aucune bonne réponse : ...
Une seule bonne réponse : ....
-
Lloicstephan dernière édition par
la probabilite de n'avoir aucune bonne repone est de 15\frac{1}{5}51 étant donne que une seule question est juste et que l'on choisit une seule question soit 4 questions fausse en conbinant 0dans1 et 1 dans 4 que l'on divise par combinaison de 1 dans 5 on obtient belle et bien 15\frac{1}{5}51
-
Lloicstephan dernière édition par
@Noemi a dit dans probabilite denombrement :
Pour chaque question, 5 réponses sont possibles donc le nombre de grilles réponses possibles est
5×5×5×5=545\times 5\times 5\times 5 =5^45×5×5×5=54Pour la question 2, quelle est la probabilité d'avoir :
aucune bonne réponse : ...
Une seule bonne réponse : ....je comprens das mon raisonnement les questions ne sont pas jointes c'est pour quoi j'ai opte au depart pour la somme!
-
Non
S'il n'y avait qu'une question, la probabilité d'avoir la bonne réponse serait de 15\dfrac{1}{5}51 donc la probabilité d'avoir une réponse fausse 45\dfrac{4}{5}54.
Vu qu'il y a 4 questions, la probabilité d'avoir aucune réponse bonne est .....
-
Lloicstephan dernière édition par
@Noemi et donc madame la probabilte d'avoir au moins deux reponses correcte est de?
parce que dans cette exercice il vaut mieux pas raisonner avec la somme!
-
Soit tu calcules pour 0 et 1 réponse juste.
Soit tu calcules pour 2, 3 et 4 réponses justes.Indique tes éléments de réponse.
-
Lloicstephan dernière édition par
etant donne qu'il y a 4 question et que la probabilite de rater une question est de 4/5
dois je faire lea somme des probabilite de rater une question ou alors le produit si oui pourquoi?
-
Si on cherche la probabilité d’un résultat OU d’un autre résultat, on ADDITIONNE les probabilités de chaque résultat possible.
Si l’on cherche la probabilité d’un résultat ET d’un autre résultat, on MULTIPLIE les probabilités de chaque résultat possible.
-
Lloicstephan dernière édition par
p(0)=454\frac{4}{5}^4544
-
Lloicstephan dernière édition par loicstephan
P(1)=1/5
en faisaint le produt on obtient
P(0)P(1)=454)</em>15{\frac{4}{5}}^4)</em>\frac{1}{5}544)</em>51
-
Oui pour p(0)
p(1)=4×15×(45)3p(1)=4\times \dfrac{1}{5}\times (\dfrac{4}{5})^3p(1)=4×51×(54)3
-
Lloicstephan dernière édition par
@Noemi je pense se que pour trouver une question ifaut qu'il ait raté 3 soit 15∗(45)3\frac{1}{5} * (\frac{4}{5})^351∗(54)3
pour quoi multiplier encore par 4?
-
4 vient du fait qu'il y à 4 questions, donc 4 choix possibles pour une bonne réponse.
-
Lloicstephan dernière édition par
@loicstephan
pouvions nous egalement faire 1−(P(1)+P(0))1- (P(1)+P(0))1−(P(1)+P(0)) ?
-
Oui, tu dois faire ce calcul.
-
Lloicstephan dernière édition par loicstephan
@Noemi soit 1−(((45)3∗15∗4)+(45)4)1- ( ((\frac{4}{5})^3 * \frac{1}{5} * 4) + (\frac{4}{5})^4)1−(((54)3∗51∗4)+(54)4)
-
Fais le calcul.
-
Lloicstephan dernière édition par
merci le calcul donne 44+4454\frac{4^4+4^4}{5^4}5444+44
-
mtschoon dernière édition par mtschoon

Bonjour,
@loicstephan , je regarde car je passe par là,
Si j'ai bien lu ce topic, tu cherches pour la question 2)
1−((P(0)+P(1))1-\biggr((P(0)+P(1)\biggr)1−((P(0)+P(1))Après calcul et simplification : P(0)+P(1)=44+4454P(0)+P(1)=\dfrac{4^4+4^4}{5^4}P(0)+P(1)=5444+44
Tu peux réduire un peu en écrivant P(0)+P(1)=2(44)54P(0)+P(1)=\dfrac{2(4^4)}{5^4}P(0)+P(1)=542(44)
La réponse que tu cherches est donc : 1−2(44)541-\dfrac{2(4^4)}{5^4}1−542(44)
-
mtschoon dernière édition par

@loicstephan ,
Si tu veux une illustration de tous les cas, tu peux faire un arbre probabiliste
Je t'en joins un.
J veut dire Réponse juste avec probabilité=1/5=0.2
F veut dire Réponse fausse avec probabilité =4/5=0.8
Tous les calculs peuvent se faire avec l'arbre.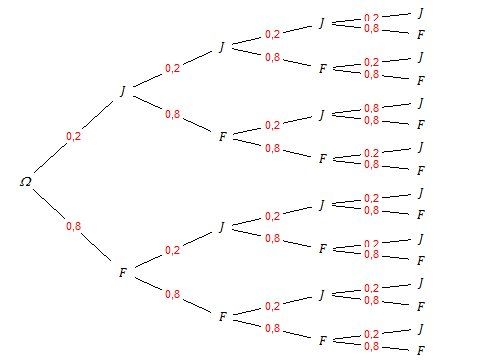
-
Lloicstephan dernière édition par loicstephan
@mtschoon dans cet arbre un chemin represente les 4 questions!
-
Oui, un chemin représente le résultat des réponses aux 4 questions.
Le résultat de la probabilité est 113625=0,1808\dfrac{113}{625}=0,1808625113=0,1808.
-
mtschoon dernière édition par mtschoon

Oui chaque chemin partant de Ω\Omega Ω et allant à l'extrémité représente les résultats des 4 questions avec les probabiltés correspondantes
Par exemple,
le chemin "supérieur" correspond à J,J,J,J avec la probabilité 0.2×0.2×0.2×0.2=0.240.2\times 0.2\times 0.2\times 0.2=0.2^40.2×0.2×0.2×0.2=0.24
le chemin juste en dessous correspond à J,J,J,F avec la probabilité 0.2×0.2×0.2×0.8=0.23×0.80.2\times 0.2\times 0.2\times 0.8=0.2^3\times 0.80.2×0.2×0.2×0.8=0.23×0.8
etc
...
etc
le chemin "inférieur" correspond à F,F,F,F avec la probabilité 0.8×0.8×0.8×0.8=0.840.8\times 0.8\times 0.8\times 0.8=0.8^40.8×0.8×0.8×0.8=0.84