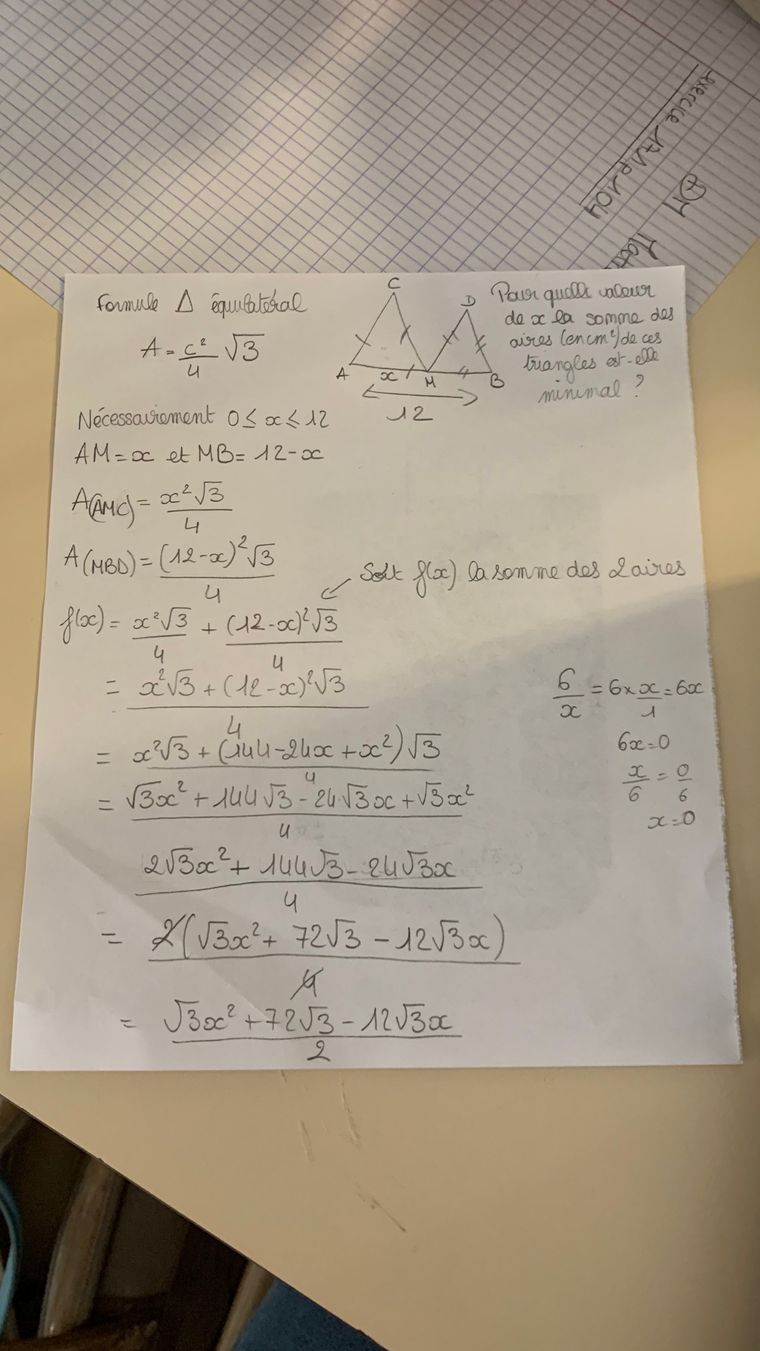DM maths exercices polynôme snd degré

Bonjour alors voilà, j'ai un exercice pour un DM que je ne comprends pas très bien pourriez vous m'aidez. Voici l'énoncer: Un segment [AB] a pour longueur 12 cm. M est un point du segment [AB] tel que AM = x (en cm). On forme sur les segments [AM] et [MB] deux triangles équilatéraux. Pour quelle valeur de x la somme des aires (en cm2) de ces triangles est-elle minimale ? Merci d'une réponse

@Cécilia-Bourgeois Bonjour,

Exprime l'aire des deux triangles en fonction de $x$ .
La hauteur d'un triangle équilatéral de côté $x$ est : $x\dfrac{\sqrt3}{2}$ .

Tu étudies ensuite la fonction correspondant à la somme des aires.

Indique tes calculs et/ou résultat si tu souhaites une vérification.

Bonjour,

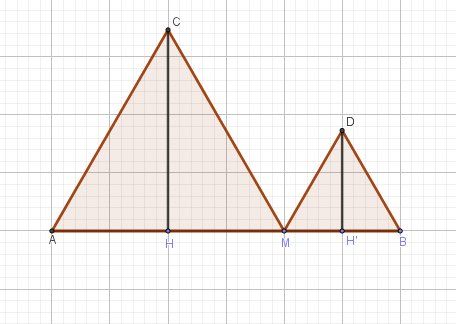
Graphique pour éclairer l'exercice.

@Cécilia-Bourgeois , bonjour,

Quelques indications complémentaires si besoin,
Condition sur $x$ : $0≤x≤120\le x\le 12$

$A M = x$
$M B = 12 - x$
$CH=x32CH=\dfrac{x\sqrt 3}{2}$
$DH′=(12−x)32DH'=\dfrac{(12-x)\sqrt 3}{2}$

Tu sais que l'aire d'un triangle est égale à $base×hauteur2\dfrac{base\times hauteur}{2}$
Tu calcules ainsi l'aire de chaque triangle, tu les ajoutes, et tu dois trouver que cette somme vaut :
$f(x)=[x2+(x−12)2]34f(x)=\dfrac{[x^2+(x-12)^2]\sqrt 3}{4}$

Tu développes le numérateur et tu le simplifies au mieux.
Tu étudies les variations de f sur [0,12] (tableau de variation) et tu tires la conclusion relative au minimum.

Sauf erreur, tu dois trouver $x = 6$ , c'est à dire M au milieu du segment [AB].

Bons calculs.

Reposte si besoin.

@mtschoon bonjour je ne comprends pas mais j'ai trouvé 6/x

@Cécilia-Bourgeois , bonjour,

Je ne sais pas à quoi tu as trouvé 6/x ....

As-tu trouvé l'expression de f(x) donnée en fonction de x ?

Merci de préciser, pour pouvoir t'aider.

@mtschoon

@Cécilia-Bourgeois ,

Tes calculs sont bons.

Tu peux éventuellement écrire :

$f(x)=32x2−63x+363f(x)=\dfrac{\sqrt 3}{2 }x^2-6\sqrt 3 x+36\sqrt 3$

Tu n'as plus qu'à étudier les variations de f

Tu as plusieurs façons, suivant tes connaissances.

Tu peux utiliser ton cours sur les polynômes du second degré de forme $f(x)=ax^2+bx+c$ avec $a≠0a\ne 0$

Ici,
$a=32a=\dfrac{\sqrt 3}{2}$
$b=−63b=-6\sqrt 3$
$c=363c=36\sqrt 3$

$a>0a\gt 0$ , dond f a un minimum pour $x=−b2ax=\dfrac{-b}{2a}$
$x=633=6x=\dfrac{6\sqrt 3}{\sqrt 3}=6$

Bien sûr, si tu connais les fonctions dérivées, tu peux aussi les utiliser.
C'est une autre méthode ( qui s'applique à toute fonction dérivable)

@Cécilia-Bourgeois ,

Si tu as besoin d'un cours sur le second degré, tu peux regarder ici :
https://www.mathforu.com/premiere-s/le-second-degre-1ere-partie/

bonsoir
comment deduisez vous que la hauteur d'un triangle equilateral de cote $x$ est $x32\frac{x \sqrt 3}{2}$

@loicstephan Bonjour,

Pour la relation, tu peux utiliser la propriété de Pythagore ou les relations trigonométriques.

Bonjour,

@loicstephan , tu as une vidéo ici qui fait la démonstration :

https://www.youtube.com/watch?v=Q_Tf_OqdlNQ

@mtschoon @Noemi merci c'est demontre par la regle de pithagore

ce qui est different lorsque le triangle est isocele

@loicstephan

Oui, cette formule ne s'applique pas si le triangle est isocèle.

Bonsoir,

@loicstephan
Cette formule relative à la hauteur est exclusivement valable pour tout triangle équilatéral