bonjour je n'arrive pas à faire un exercice de maths. Je dois déterminer une expression de f(x) en sachant que f(0) =25; f(5) = 0 et f(25) =0. Pouvez-vous m'aider s'il vous plaît.
-
Zaloxy _ dernière édition par
bonjour je n'arrive pas à faire un exercice de maths.
Je dois déterminer une expression de f(x) en sachant que f(0) =25; f(5) = 0 et f(25) =0.
Pouvez-vous m'aider s'il vous plaît.
-
mtschoon dernière édition par

@Zaloxy-_ , bonjour,
Ta question est incomplète car tu ne donnes pas la nature de f
-
Zaloxy _ dernière édition par
Excusez-moi, f est une fonction définie par ax²+bx+c.
-
mtschoon dernière édition par mtschoon

@Zaloxy-_ , daccord mais revois aussi tes données.
f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c avec a≠0a\ne 0a=0
f(0)=25f(0)=25f(0)=25 <=> c=25c=25c=25Mais... f(5)=0f(5) = 0f(5)=0 et f(25)=0f(25) =0f(25)=0. me laisse perplexe...
Es-tu bien sûr ?
Vérifie.
-
Zaloxy _ dernière édition par
Il faut remplacer f(25) =0 par f(20) =0 et je possède seulement ces données. Mais je peux déduire que f(25) = 25, mais l'énoncer ne me donne pas cette information c'est pour ça que je ne l'ai pas utilisé.
-
mtschoon dernière édition par mtschoon

@Zaloxy-_ , tu as donc changé ton énoncé !
Si je résume, tu as finalement :
f(0)=25f(0)=25 f(0)=25 <=> c=25c=25c=25donc f(x)=ax2+bx+25f(x)=ax^2+bx+25f(x)=ax2+bx+25
et puis, f(5)=0f(5)=0f(5)=0 et f(20)=0f(20)=0f(20)=0
f(5)=0f(5)=0f(5)=0 <=> 25a+5b+25=025a+5b+25=025a+5b+25=0
f(20)=0f(20)=0f(20)=0 <=> 400a+20b+25=0400a+20b+25=0400a+20b+25=0Pour trouver aaa et bbb, tu résous le système :
{25a+5b+25=0400a+20b+25=0\begin{cases}25a+5b+25=0\cr 400a+20b+25=0\end{cases}{25a+5b+25=0400a+20b+25=0
Tu peux simplifier un peu chaque équation puis tu resous par combinaison ou substutution.
Sauf erreur, tu dois trouver a=14a=\dfrac{1}{4}a=41 et b=−254b=-\dfrac{25}{4}b=−425, d'où
f(x)=14x2−254x+25f(x)=\dfrac{1}{4}x^2-\dfrac{25}{4}x+25f(x)=41x2−425x+25
Bons calcul.
Reposte si besoin.
-
mtschoon dernière édition par

Illustration graphique
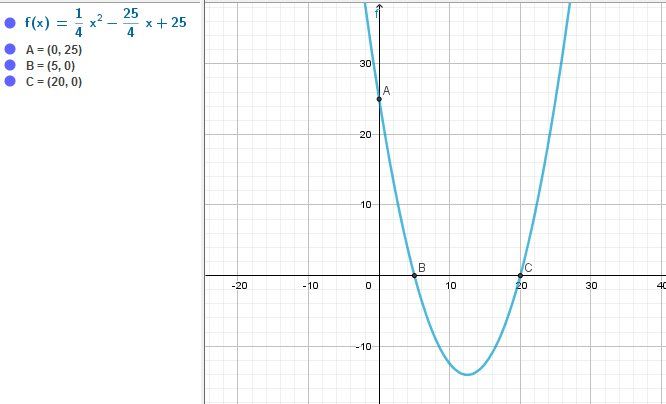
-
Zaloxy _ dernière édition par
@mtschoon Excusez-moi mais quelle est la démarche à suivre pour résoudre un système, le terme système ne me dit rien.
-
mtschoon dernière édition par

@Zaloxy-_ , je te mets un lien, mais c'est du cours de 3ème.
https://www.mathforu.com/troisieme/resolution-de-systemes-d-equations/
-
mtschoon dernière édition par mtschoon

Piste possible,
En simplifiant la première équation, tu peux écrire : 5a+b=−55a+b=-55a+b=−5, c'est à dire b=−5a−5b=-5a-5b=−5a−5
La seconde équation peut s'écrire 80a+4b=−580a+4b=-580a+4b=−5
Dans cette seconde équation , tu remplaces bbb par −5a−5-5a-5−5a−5
En résolvant, tu trouveras bbb et tu en déduiras aaa
Cette méthode s'appelle méthode par substitution.
-
Zaloxy _ dernière édition par
@mtschoon Je vous remercie pour toute l'aide que vous m'avez apporter.
Bonne soirée
-
mtschoon dernière édition par

De rien @Zaloxy-_ et bon travail .
-
@Zaloxy-_ Bonjour,
Une méthode qui n'utilise pas un système de deux équations à deux inconnues.
Puisque f(5)=0f(5)= 0f(5)=0, x−5x-5x−5 est un facteur de fff;
Puisque f(20)=0f(20)= 0f(20)=0, x−20x-20x−20 est un facteur de fff.
Donc la fonction peut s'écrire : f(x)=a(x−5)(x−20)f(x) = a(x-5)(x-20)f(x)=a(x−5)(x−20)
Comme f(0)=25f(0)=25f(0)=25
Il reste à résoudre : 100a=25100a= 25100a=25, d'ou a=....a= ....a=....
En développant on retrouve l'expression de la fonction sous la forme :
f(x)=14x2−254x+25f(x) = \dfrac{1}{4}x^2-\dfrac{25}{4}x+25f(x)=41x2−425x+25