Déterminer un polynôme de second degré
-
Llotus21 dernière édition par Noemi
Bonjour.
Je voudrais savoir comment déterminer un polynôme de second degré dont p(0)=3 et ses deux racines sont -2 et 3/2 ?
-
@lotus21 Bonjour,
Si -2 est une racine du polynôme, alors x+2x+2x+2 est un facteur du polynôme.
Si 32\dfrac{3}{2}23 est une racine du polynome, alors ....
le polynôme peut s'écrire p(x)=a(x+2)(x...)p(x)=a(x+2)(x...)p(x)=a(x+2)(x...)Pour déterminer aaa, tu utilises p(0)=3p(0)=3p(0)=3.
Indique tes calculs et/ou résultats si tu souhaites une vérification.
-
Lloicstephan dernière édition par loicstephan
@Noemi a dit dans Déterminer un polynôme de second degré :
Pour déterminer aaa, tu utilises p(0)=3p(0)=3p(0)=3.
Bonjour une autre methode consistera a passer par lasomme des deux racine
on sait que x1+x2=−bax_1 + x_2 = - \frac{b}{a}x1+x2=−ab tu obtiens −ba=−12- \frac{b}{a} = - \frac{1}{2}−ab=−21
ce qui doonne l'equation −2b+a=0-2b+a=0−2b+a=0 tu connais bbb tu determines aaa
-
Une erreur de signe. Quelle est la valeur de bbb ?
-
Lloicstephan dernière édition par
@Noemi a dit dans Déterminer un polynôme de second degré :
Une erreur de signe. Quelle est la valeur de b ?
partant de la formule de la somme des deux racines on a bien
x1+x2=−bax_1+ x_2= − \frac{b}{a} x1+x2=−ab or la somme des ses racines (racinnes donnees dans la consigne) donne bien −2+32=−4+32=−12-2+ \frac{3}{2}=\frac{-4+3}{2}=- \frac{1}{2}−2+23=2−4+3=−21
soit −12=−ba- \frac{1}{2}=− \frac{b}{a}−21=−ab
je ne vois pas d'erreur de signe madame ! par developpement de l'eexpression factorisée elle obtiendra b=12b= \frac{1}{2}b=21
-
La méthode est correcte.
Pour p(x)p(x)p(x) de la forme p(x)=ax2+bx+cp(x)=ax^2+bx+cp(x)=ax2+bx+c
A partir de p(0)=3p(0)= 3p(0)=3, on déduit c=3c= 3c=3A partir de x1×x2=ca=−3x_1\times x_2= \dfrac{c}{a}=-3x1×x2=ac=−3, on déduit a=−1a = -1a=−1
puis avec x1+x2=−ba=−12x_1+x_2= -\dfrac{b}{a}=-\dfrac{1}{2}x1+x2=−ab=−21, on déduit b=−12b= -\dfrac{1}{2}b=−21.
Soit p(x)=−x2−12x+3p(x) = -x^2-\dfrac{1}{2}x+3p(x)=−x2−21x+3.
Avec l'autre méthode :
Si −2-2−2 est une racine du polynôme, alors (x+2)(x+2)(x+2) est un facteur du polynôme.
Si 32\dfrac{3}{2}23 est une racine du polynôme, alors (x−32)(x-\dfrac{3}{2})(x−23) est un facteur du polynôme.
Le polynôme peut s'écrire p(x)=a(x+2)(x−32)p(x)=a(x+2)(x-\dfrac{3}{2})p(x)=a(x+2)(x−23)Pour déterminer aaa, on utilise p(0)=3p(0)=3p(0)=3
Soit −3a=3-3a= 3−3a=3; d'ou a=−1a=-1a=−1
p(x)=−(x+2)(x−32)p(x)=-(x+2)(x-\dfrac{3}{2})p(x)=−(x+2)(x−23) en développant
p(x)=−x2−12x+3p(x)= -x^2-\dfrac{1}{2}x+3p(x)=−x2−21x+3
-
Lloicstephan dernière édition par
@loicstephan a dit dans Déterminer un polynôme de second degré :
je ne vois pas d'erreur de signe madame ! par developpement de l'eexpression factorisée elle obtiendra b=12b= \frac{1}{2}b=21
ell ne doit donc pas proceder par developpement de l'expression factorisee tant qu'elle n'a pas la valeur de a qui pourrait changer tous les signes! l'ideal c'est la methode des relations entres les solution !
qu'en pensez vous ?
-
Lloicstephan dernière édition par
Ce message a été supprimé !
-
Pour moi, les deux méthodes sont équivalentes. Peut-être voir qu'elle est la plus rapide et/ou la moins source à erreur.
-
mtschoon dernière édition par mtschoon

Bonjour,
Je crois qu'il n'y a pas de bonnes ou mauvaises méthodes .
Il y a des méthodes différentes, c'est tout.Dans la mesure où deux points ont des ordonnées nulles, j'imagine (?) que le professeur qui a donné le sujet a pensé à la méthode par factorisation.
Vu que deux méthodes sont données, j'en mets une troisième.
Pas plus courte, mais qui a l'avantage d'être générale, applicable quelles que soient les coordonnées des points donnés.J'appelerais ça la "mise en équations de l'énoncé":
système de 3 équations du premier degré à 3 inconnues.p(x)=ax2+bx+cp(x)=ax^2+bx+cp(x)=ax2+bx+c
p(0)=3p(0)=3p(0)=3 <=> c=3\boxed{c=3}c=3 donc p(x)=ax2+bx+3p(x)=ax^2+bx+3p(x)=ax2+bx+3
p(−2)=0p(-2)=0p(−2)=0 <=>4a−2b+3=04a-2b+3=04a−2b+3=0 <=> 2b=4a+3\boxed{2b=4a+3}2b=4a+3
p(32)=0p(\dfrac{3}{2})=0p(23)=0 <=> 94a+32b+3=0\dfrac{9}{4}a+\dfrac{3}{2}b+3=049a+23b+3=0 <=> 3a+2b+4=0\boxed{3a+2b+4=0}3a+2b+4=0
Substitution : en remplaçant 2b2b2b par 4a+34a+34a+3 dans la dernière équation, on trouve a=−1a=-1a=−1 puis b=−12b=-\dfrac{1}{2}b=−21
Conclusion :
p(x)=−x2−12x+3\boxed{p(x)=-x^2-\dfrac{1}{2}x+3}p(x)=−x2−21x+3
-
mtschoon dernière édition par

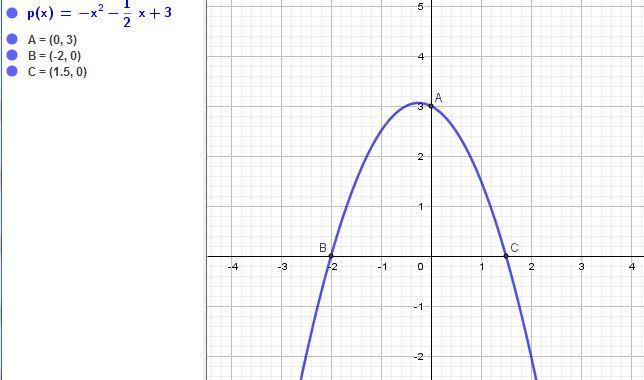
Graphique