Le nombre de solutions de l'équation
-
BBarrak dernière édition par Noemi
Bonjour,
j'ai besoin d'aide , dans mon DM , il y a 2 questions , ce serait vraiment simpa de m'aider .. je vous remercie d'avance ..Scan supprimé par la modération.
- Etudier suivant la valeur du réel a le nombre de solutions de l'équation ex=x+ae^x = x + aex=x+a.
- Déterminer une suite définie sur N, strictement positive et strictement monotone dont la somme des 100 premiers termes vaut 1.
-
@Barrak Bonjour,
Un seul exercice par post, donc propose le deuxième dans un autre sujet.
Pour l'exercice 1, traces les deux fonctions f(x)=exf(x) = e^xf(x)=ex et g(x)=xg(x) = xg(x)=x, puis tu analyses la position de la fonction ggg par rapport à la fonction fff en faisant varier aaa.
-
DDarius dernière édition par
@Barrak Bonjour, stp comment tu fais pour envoyer une image...?
-
mtschoon dernière édition par mtschoon

Bonjour,
@Barrak , le texte aurait dû être écrit la main...
Une proposition alternative pour la première question.
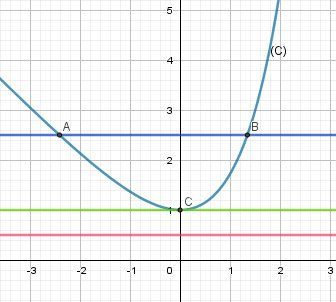
Soit f(x)=ex−xf(x)=e^x-xf(x)=ex−x
Cette fonction est facile à étudier sur RRR ( sa dérivée vaut $ f′(x)=exf'(x)=e^xf′(x)=ex.
Son minimum est pour x=0 et il vaut 1.
Soit (C) sa représentation graphique.
Soit (D) la droite parallèle à l'axe des abscissses d'équation y=ay=ay=aOn cherche, suivant a, le nombre de points d'intersection de de (C) avec (D) :
Pour a<1\boxed{a\lt 1}a<1 aucun point d'intersection donc aucune solution à l'équation ex−x=ae^x-x=aex−x=a
Pour a=1\boxed{a = 1}a=1 un point d'intersection (de coordonnées (0,1), donc une solution à l'équation ex−x=ae^x-x=aex−x=a (qui est 0)
Pour a>1\boxed{a\gt 1}a>1 ........................................................................(tu complètes)
-
mtschoon dernière édition par

@Barrak , schéma :