Repères et coordonnées

Bonjour à tous sur ce forum de math!

Je vous écris car je dois résoudre un problème au sujet des repères et coordonnées et je suis perdue.
Il y a une figure composée de O A B E1 et E2 sur une grille (voir image en pièce jointe).

Par rapport à cette figure, je dois:
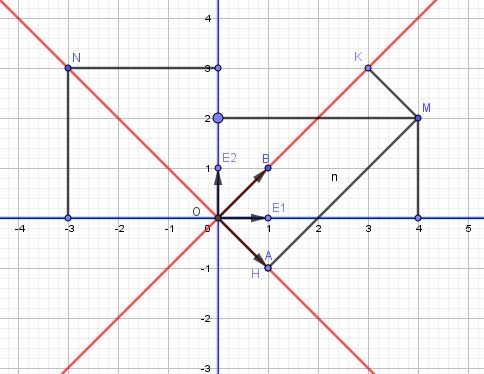
a) Représenter les points dont les coordonnées relativement au repère R1 = (O;E1,E2) sont M (4;2) et N (-3;3).
b) Trouver les coordonnées de ces points relativement au repère R2 = (O;A;B).

Je crois savoir que:

les points à trouver sont dans R1;
(4;2) sont les coordonnées dans R1;
4 est l'abscisse et 2 est l'ordonnée de M;

Mais, je ne comprends pas:

Comment représenter les points sur cette grille qui n'a aucune valeur;
Comment trouver les coordonnées s'il y a un changement de repère?
Aussi, la réponse pour l'exercice b) est M(1;3) et N (3;0) mais je ne sais pas comment y parvenir.

Est-ce que quelqu'un du forum a déjà vu ce type de problème et pourrait m'éclairer pour le résoudre?

Bonne soirée à tous!
Floflo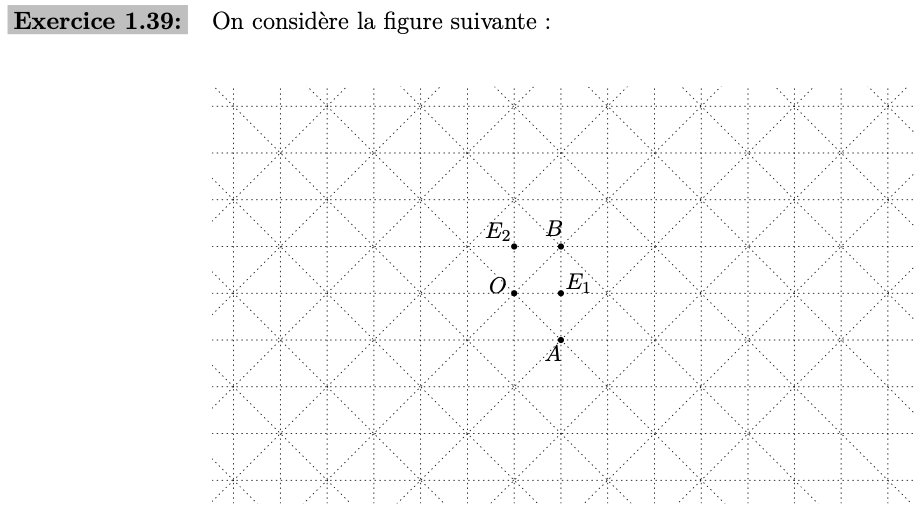

Screenshot 2021-11-05 at 00.51.32.png

@Flo-Flo Bonsoir,

Dans le repère $R_1= (0;E_1;E_2)$ , le point $E_1$ a pour coordonnées $(1; 0)$ et le point $E_2$ ; $(0; 1)$ .

Bonjour @Noemi et merci pour votre réponse. Par contre, j'ai cru comprendre que je devais trouver M et N dans le repère R2, et c'est ça qui me bloque... car je ne comprends pas ce qu'est le repère R2... mais peut-être que je n'ai même pas compris consigne...

@Flo-Flo , bonjour,

Je te mets un schéma pour essayer de t'éclairer.

@Flo-Flo ,

Sur le schéma que je viens de t'indiquer :

Le repère R1 est en bleu : O origine et vecteurs unitaires $OE1→\overrightarrow{OE1}$ et $OE2→\overrightarrow{OE2}$

Le repère R2 est en rouge : O origine et vecteurs unitaires $OA→\overrightarrow{OA}$ et $OB→\overrightarrow{OB}$

$OM→=4OE1→+2OE2→\overrightarrow{OM}=4\overrightarrow{OE1}+2\overrightarrow{OE2}$
$ON→=−3OE1→+3OE2→\overrightarrow{ON}=-3\overrightarrow{OE1}+3\overrightarrow{OE2}$

Les coordonnées de M dans le repère R2 son(x,y) qui vérifient : $OM→=xOA→+yOB→\overrightarrow{OM}=x\overrightarrow{OA}+y\overrightarrow{OB}$

Il faut donc que tu trouves x et y

Pistes,
$OA→=1OE1→−1OE2→\overrightarrow{OA}=1\overrightarrow{OE1}-1\overrightarrow{OE2}$
$OB→=1OE1→+1OE2→\overrightarrow{OB}=1\overrightarrow{OE1}+1\overrightarrow{OE2}$
En ajoutant membre à membre
$OA→+OB→=2OE1→\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OE1}$
En retranchant membre à membre
$OB→−OA→=2OE2→\overrightarrow{OB}-\overrightarrow{OA}=2\overrightarrow{OE2}$
Tu peux déduire que
$OE1→=12OA→+12OB→\overrightarrow{OE1}=\dfrac{1}{2}\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB}$
$OE2→=−12OA→+12OB→\overrightarrow{OE2}=-\dfrac{1}{2}\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB}$
Vu que : $OM→=4OE1→+2OE2→\overrightarrow{OM}=4\overrightarrow{OE1}+2\overrightarrow{OE2}$ , tu remplaces $OE1→\overrightarrow{OE1}$ et $OE2→\overrightarrow{OE2}$ par les expressions qui viennent d'être trouvées , d'où:
$OM→=4(12OA→+12OB→)+2(−12OA→+12OB→)\overrightarrow{OM}=4(\dfrac{1}{2}\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB})+2(-\dfrac{1}{2}\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB})$
Tu transformes et tu dois trouver :
$OM→=1OA→+3OB→\boxed{\overrightarrow{OM}=1\overrightarrow{OA}+3\overrightarrow{OB}}$
Les coordonnées de M dans le repère R2 sont (1,3), ce que tu peux vérifier sur le schéma.

Regarde cela de près et lorsque tu as bien maîtrisé, tu peux calculer les coordonnées de N dans R2, de la même façon.

Waoh, merci infiniment @mtschoon !!! Sans votre schéma qui a dû vous prendre du temps à réaliser, je n'aurais pas compris!! J'ai maintenant compris comment trouver M et N, merci beaucoup!!!! Bonne soirée, Flo-flo

C'est parfait @Flo-Flo , si je t'ai éclairée.
Bonne soirée à toi.