Terminale, Spé Maths, Lecture Graphique
-
Mmaariuuuus dernière édition par maariuuuus
Bonjour, j’ai un devoir maison à faire pour mercredi cependant je n’arrive pas à faire l’exercice 1. Car à chaque question le professeur demande de justifié, cela me bloque si une personne pourrait m’aider merci..
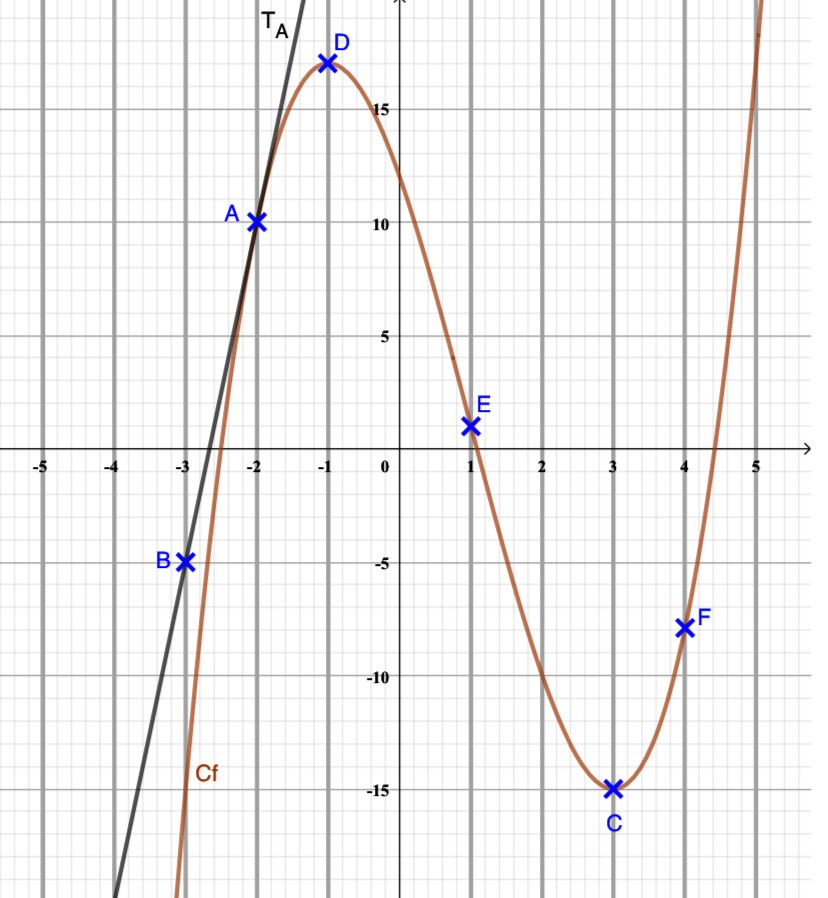
La droite TA est la tangente a Cf en son point A(−2 ; 10). On admet que TA passe aussi par le point B(−3 ; −5).
Les points C et des D sont des points de Cf d’abscisse respective 3 et −1. On admet que la tangente a Cf en C et en D est parallele a l’axe des abscisses.
Les points E et F sont des points de Cf d’abscisse respective 1 et 4.- Donner le nombre de solution reelle de l’ ́equation f(x) = 0. Justifier.
D’après le graphique l’ensemble des solutions de l’équation f(x)=0 est S={-2,5; 1,1; 4,4}
- D ́eterminer le nombre de solution de l’ ́equation f’(x) = 0. Justifier.
2 solutions : x=-1 et x=3
-
D ́eterminer le signe de f′(1) et de f′(4). Justifier.
-
Dresser le tableau de signes de f′(x) pour x ∈ R. Justifier.
Vous avez en ci-joint
 la courbe représentative
la courbe représentative
-
Mmaariuuuus dernière édition par
Ce message a été supprimé !
-
@maariuuuus Bonjour,
Indique tes éléments de réponse et la question qui te pose problème.
-
Les solutions de l'équation f(x)=0f(x)= 0f(x)=0 correspondent aux points d'intersection de la courbe avec la droite y=0y=0y=0, soit l'axe des abscisses. Donc ..... solutions.
-
Si f′(x)f'(x)f′(x)= 0, la tangente est horizontale, soit parallèle à l'axe des abscisses.
-