Géométrie dans l’espace.

Bonjour,
J’ai un exercice à réaliser mais j’ai quelque difficulté.
Voici l’exercice:
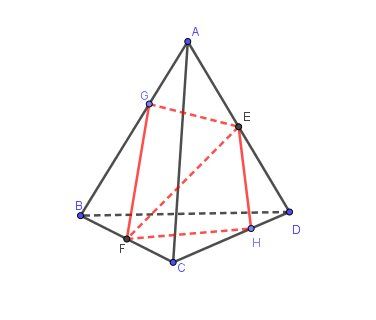
On considère un tétraèdre ABCD de l'espace. On note E et F les milieux respectifs de [AD] et [BC] et on définit les points G et H par:
vecteur(AG )= 1/3vecteur(AB) et vecteur(CH) = 2/3vecteur(CD)
Démontrer que les points E, F, G et H son coplanaires.

Merci d’avance pour votre aide.

@Marco93 , re-bonsoir,

Cet exercice est dans le même esprit que l'exercice précédent sur le cube.
Tu dois appliquer la même méthode.

Je joins une image pour plus de clarté.

98d38024-17eb-4e65-b5a0-bd813a68414a-tétraère.jpg

@mtschoon
Re-bonsoir, j’ai bien compris qu’il fallait que je démontre que les 4 points sont dans le même plan mais je ne vois toujours pas par où commencer car dans les exercices que j’ai déjà fait on nous donne les coordonnées ou une égalité à démontrer, je ne sais pas quel vecteur choisir?

@Marco93 ,

Je te donne des indications ( et regarde ton topic précédent)

Avec la relation de Chasles, tu exprimes $EF→\overrightarrow{EF}$ , $EF→\overrightarrow{EF}$ , $EH→\overrightarrow{EH}$ en fonction de $AB→\overrightarrow{AB}$ , $AC→\overrightarrow{AC}$ , $AD→\overrightarrow{AD}$ .

Sauf erreur, tu dois trouver :

$EF→=12AB→+12AC→−12AD→\overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AD}$

$EG→=13AB→−12AD→\overrightarrow{EG}=\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}$

$EH→=13AB→+16AD→\overrightarrow{EH}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}$

E , F, G , H coplanaires <=> il existe les réels a, b tels que : $EF→=aEG→+bEH→\overrightarrow{EF}=a\overrightarrow{EG}+b\overrightarrow{EH}$

Comme dans l'exercice précédent , tu auras un système d'inconnues a et b à résoudre, mais cette fois, il ne sera pas impossible.

Tu trouveras une valeur pour a et une valeur pour b.

@Marco93 ,

Je viens de faire le calcul rapidement.

Sauf erreur, tu dois trouver $a=32a=\dfrac{3}{2}$ et $b=32b=\dfrac{3}{2}$

Donc

$EF→=32EG→+32EH→\overrightarrow{EF}=\dfrac{3}{2}\overrightarrow{EG}+\dfrac{3}{2}\overrightarrow{EH}$

Conclusion : E,F,G,H coplanaires.

Bon travail ( dans cet exercice, tu as du travail !)